Наша команда-партнер Artmisto
Вызначэння. Хай патрабуецца вырашыць задачу (2): f (x) -> min, х Аб Rn (2) У двухмернай пространтсве R2 рашэнню такой задачы можна даць геаметрычную ілюстрацыю. Хай кропка х = (х1, х2) ляжыць на плоскасці Ох1х2. Ўвядзем трэцюю каардынату х3 так, каб вось каардынатаў Ох3 была перпендыкулярная плоскасці Ох1х2 (мал.1). Раўнанні х3 = f (х1, х2) адпавядае паверхню ў трохмернай прасторы.
Калі функцыя f (х) дасягае лакальнага мінімуму ў кропцы х * О R2, то паверхня ў некаторай наваколлі кропкі х * мае форму чары (мал.1).
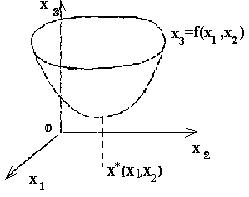
мал.1
Нагадаем, што лініямі ўзроўню функцыі f (х1, х2) называюць сямейства ліній плоскасці R2, на якіх функцыя прымае пастаяннае значэнне. Няяўнай раўнаннем лініі ўзроўню з'яўляецца раўнанне f (x1, x2) = C. Калі функцыя f (x) мае ў R2 адзіную кропку лакальнага мінімуму
х * (х * 1, х * 2), то такая функцыя называецца мономодальной. Ўзаемнае размяшчэнне яе ліній ўзроўню мае выгляд, намаляваны на мал.2.
Мультымадальны называюцца функцыі, якія маюць больш аднаго экстрэмуму. Такая, напрыклад, функцыя Химмельблау
F (x) = (x12 + x2-11) 2+ (x1 + x22-7) 2,
якая мае чатыры ізаляваныя пункту мінімуму. На мал.3 схематычна намаляваны лініі ўзроўню гэтай функцыі.
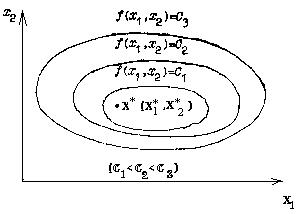
мал.2
Каб знайсці кропку х * лакальнага мінімуму функцыі f (х), складаюць паслядоўнасць кропак (набліжэнняў да вырашэння) {х (k)} (k = 0,1, ...), што сыходзіў да кропкі х *
(K = 0,1, ...), што сыходзіў да кропкі х *.
Паслядоўнасць значэнняў функцыі f (х (k)) павінна быць манатонна меншае і абмежаванай знізу:
f (x (0))> = f (x (1))> =. . . > = F (x (k))> =. . . > = F (x (*)).
Геаметрычны вобраз рашэння задачы (2) для выпадку двух зменных нагадвае спуск на дно чары. Гэта матывуе назвы метадаў рашэння задачы (2) - «метады спуску».
Для розных метадаў спуску спачатку выбіраюць пачатковую кропку паслядоўнасці х (0). Далейшыя набліжэння х (k) вызначаюцца суадносінамі
x (k + 1) = x (k) + t (k) S (k) (k = 0, 1, 2,...), (12)
Дзе S (k) - вектар напрамкі спуску; скалярная велічыня t (k) я | вляется рашэннем задачы аднамернай мінімізацыі
f (x (k) + ts (k)) -> min, t Аб R. (13)
Такім чынам, задача пошуку мінімуму функцыі некалькіх зменных зводзіцца да паслядоўнасці задач аднамернай мінімізацыі (13) па зменнай t на адрэзках n-мернага прасторы, якія праходзяць праз кропкі х (k) у напрамку вектараў S (k).
Метады спуску адрозніваюцца выбарам вектару спуску і спосабам юшения задачы аднамернай мінімізацыі.
Пры вырашэнні паслядоўнасці задач (12) можна абмежавацца метадам сканавання для пошуку мінімуму функцыі адной переменюй. Выбраўшы адвольна пачатковую кропку х (0) і памер начальюго кроку h па зменнай t, у метадзе сканавання можна атрымаць розныя пункты мінімуму Мультымадальны функцыі.
Калі функцыя f (x) мономодальна, то незалежна ад выбару пачатковай кропкі траекторыя пошуку павінна прывесці да адзінай кропцы лакальнага мінімуму гэтай функцыі.
Пераважная колькасць рэальных задач аптымізацыі, якія прадстаўляюць практычны цікавасць, з'яўляюцца шматмерным: у іх мэтавая функцыя залежыць ад некалькіх аргументаў, прычым часам іх колькасць можа быць вельмі вялікім.
Успомнім, напрыклад, задачу аб хімічным вытворчасці. Мы адзначылі, што ў ёй мэтавая функцыя залежыць ад тэмпературы, і пры пэўным яе выбары прадукцыйнасць (выхад цікавіць нас прадукту) аказваецца максімальнай. Аднак, разам з тэмпературай, прадукцыйнасць залежыць таксама ад ціску, суадносін паміж канцэнтрацыямі уводзімага сыравіны, каталізатараў і шэрагу іншых фактараў. Такім чынам, задача выбару найлепшых умоў хімічнай вытворчасці - гэта тыповая шматмерных задача аптымізацыі. Матэматычная пастаноўка "такіх задач аналагічная іх пастаноўцы ў аднамернай выпадку: шукаецца найменшую (найбольшая) значэнне мэтавай функцыі, зададзенай на некаторай мностве Е магчымых значэнняў яе аргументаў. У выпадку, калі целевля функцыя бесперапынная, а мноства Е з'яўляецца замкнёнай абмежаванай вобласцю, застаецца справядлівай тэарэма Веерштрас. Тым самым вылучаецца клас задач аптымізацыі, для якіх гарантавана існаванне рашэння. У далейшым мы заўсёды будзем меркаваць, ня абумаўляючы гэтага асабліва, што ўсё глядзяць, ыя задачы належаць гэтаму класу. Як і ў аднамернай выпадку, характар задачы і адпаведна магчымыя метады рашэння істотна залежаць ад той інфармацыі аб мэтавай функцыі, якая нам даступная ў працэсе яе даследавання. У адных выпадках мэтавая функцыя задаецца аналітычнай формулай, з'яўляючыся пры гэтым духавых станаў . Тады можна вылічыць яе прыватныя вытворныя, атрымаць відавочнае выраз для градыенту, які вызначае ў вызначальнага ў кожным пункце, напрамкі ўзрастання і змяншэння функцыі,

Мал. 1.
Пабудова сеткі з крокам h і выбар "пробных" кропак у вузлах сеткі для набліжанага вызначэння найменшага значэння функцыі дзвюх зменных. і выкарыстоўваць гэтую інфармацыю для вырашэння задачы. У іншых выпадках ніякай формулы для мэтавай функцыі няма, а ёсць толькі магчымасць вызначыць яе значэнне ў любым пункце разгляданай вобласці (з дапамогай разлікаў, у выніку эксперыменту і т. Д.). У такіх задачах у працэсе вырашэння мы фактычна можам знайсці значэння мэтавай функцыі толькі ў канчатковым ліку кропак, і па гэтай інфармацыі патрабуецца набліжана ўсталяваць яе найменшае значэнне для ўсёй вобласці. Шматмерныя задачы, натуральна, з'яўляюцца больш складанымі і працаёмкімі, чым аднамерныя, прычым звычайна цяжкасці пры іх вырашэнні ўзрастаюць пры павелічэнні памернасці. Для таго каб вы лепш адчулі гэта, возьмем самы просты па сваёй ідэі набліжаны метад пошуку найменшага значэння функцыі, які ўжо абмяркоўваўся для аднамерных задач ст. Кроем разгляданую вобласць сеткай з крокам h (мал. 1) і вызначым значэння функцыі ў яе вузлах. Параўноўваючы атрыманыя колькасці паміж сабой, знойдзем сярод іх найменшую і прымем яго набліжана за найменшае значэнне функцыі для ўсёй вобласці. Як мы ўжо казалі вышэй, дадзены метад выкарыстоўваецца для вырашэння аднамерных задач. Часам ён ужываецца таксама для вырашэння двухмерных, радзей трохмерных задач. Аднак для задач большай памернасці ён практычна непрыдатны з-за занадта вялікага часу, неабходнага для правядзення разлікаў. Сапраўды, выкажам здагадку, што мэтавая функцыя залежыць ад пяці зменных, а абсяг вызначэння з'яўляецца пятимерным кубам, кожны бок якога пры пабудове сеткі мы дзелім на 40 частак. Тады агульная колькасць вузлоў сеткі будзе роўна 415 ~ 108. Хай вылічэнне значэння функцыі ў адным пункце патрабуе 1000 арыфметычных аперацый (гэта крыху для функцыі пяці зменных). У такім выпадку, агульная колькасць аперацый складзе 1011. Калі ў нашым распараджэнні маецца ЭВМ з хуткадзейнасцю за 1 млн. Аперацый у секунду, то для вырашэння задачы з дапамогай дадзенага метаду спатрэбіцца 105 секунд, што перавышае суткі бесперапыннай працы. Даданне яшчэ адной незалежнай зменнай павялічыць гэты час у 40 разоў. Праведзеная ацэнка паказвае, што для вялікіх задач аптымізацыі метад суцэльнага перабору непрыдатны. Часам суцэльны перабор замяняюць выпадковым пошукам. У гэтым выпадку пункту сеткі праглядаюцца ня запар, а ў выпадковым парадку. У выніку пошук найменшага значэння мэтавай функцыі істотна паскараецца, але губляе сваю надзейнасць.
Метад покоординатного спуску.
Хай трэба знайсці найменшае значэнне мэтавай функцыі u = f (M) = f (x 1, x 2,..., Xn). Тут праз М пазначаная кропка n-мернага прасторы з каардынатамі x 1, x 2,. . . , xn: M = (x 1, x 2,..., xn). Абярэм якую-небудзь пачатковую кропку М 0 = (x 10, x 20,..., Xn0) і разгледзім функцыю f пры фіксаваных значэннях ўсіх зменных, акрамя першай: f (x 1, x 20, x 30,..., xn0). Тады яна ператворыцца ў функцыю адной зменнай x 1. Змяняючы гэтую зменную, будзем рухацца ад пачатковай кропкі x 1 = x 10 у бок змяншэння функцыі, пакуль не дойдзем да яе мінімуму пры x 1 = x 11, пасля якога яна пачынае ўзрастаць. Кропку з каардынатамі (x 11, x 20, x 30,..., Xn0) абазначым праз М 1, пры гэтым f (M0)> = f (M 1). Фіксуем цяпер зменныя: x 1 = x 11, x 3 = x 30,. . . , xn = xn0 і разгледзім функцыю f як функцыю адной зменнай x 2: f (x 11, x 22, x 30..., xn0). Змяняючы x 2, будзем зноў рухацца ад пачатковага значэння x2 = x20 ў бок змяншэння функцыі, пакуль не дойдзем да мінімуму пры x2 = x21 .Точку з каардынатамі {x 11, x 21, x 30. . . xn0} абазначым праз М 2, пры гэтым f (M1)> = f (M 2).
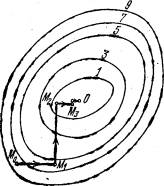
Мал. 2. Пошук найменшага значэння функцыі метадам покоординатного спуску.
Правядзем такую ж мінімізацыю мэтавай функцыі па пераменным x 3, x 4,. . . , xn. Дайшоўшы да зменнай xn, зноў вернемся да x 1 і працягнем працэс. Гэтая працэдура цалкам апраўдвае назву метаду. З яе дапамогай мы пабудуем паслядоўнасць кропак М 0, М 1, М 2,. . . , Якой адпавядае манатонная паслядоўнасць значэнняў функцыі f (M0)> = f (M 1)> = f (M 2)> = ... Абрыў яе на некаторай кроку k можна набліжана прыняць значэнне функцыі f (Mk) за яе найменшае значэнне ў разгляданай вобласці. Адзначым, што дадзены метад зводзіць задачу пошуку найменшага значэння функцыі некалькіх зменных да шматразовага рашэнню аднамерных задач аптымізацыі. Калі мэтавая функцыя f (x 1, x 2, ..., xn) зададзена відавочнай формулай і з'яўляецца дыферэнцыруемых, то мы можам вычисллить яе прыватныя вытворныя і выкарыстоўваць іх для вызначэння напрамкі змяншэння функциипо кожнай зменнай і пошуку адпаведных аднамерных мінімумаў. У адваротным выпадку, калі відавочнай формулы для мэтавай функцыі няма, аднамерныя задачы варта вырашаць з дапамогай аднамерных метадаў. На мал. 2 намаляваныя лініі ўзроўню некаторай функцыі дзвюх зменных u = f (х, у). Уздоўж гэтых ліній функцыя захоўвае пастаянныя значэння, роўныя 1, 3, 5, 7, 9. Паказана траекторыя пошуку яе найменшага значэння, якое дасягаецца ў кропцы Аб, з дапамогай метаду покоординатного спуску. Пры гэтым трэба ясна разумець, што малюнак служыць толькі для ілюстрацыі метаду. Калі мы пачынаем да вырашэння рэальнай задачы аптымізацыі, такога малюнка, які змяшчае ў сабе гатовы адказ, у нас, вядома, няма. Хай патрабуецца вырашыць задачу (2):
f (x) -> min, х ОRn. (2)
У двухмернай пространтсве R2. Рашэнне задачы (2) метадам покоординатного спуску, інакш званага метадам Гаўса - Зейделя, вырабляюць па наступнай агульнай схеме.
Выбіраюць адвольна пачатковую кропку х (0) з вобласці вызначэння функцыі f (х). Набліжэння х (k) вызначаюцца суадносінамі (3):
x (k + 1) = x (k) + t (k) S (k) (k = 0,1,2, ...),
дзе вектар напрамкі спуску s (k) - гэта адзінкавы вектар, які супадае з якім-небудзь каардынатных напрамкам (напрыклад, калі S (k) паралеляў х1, то S (k) = {1,0,0, ..., 0} , калі ён паралеляў x2, то S (k) = {0, 1, 0,..., 0} і г.д.); велічыня t (k) з'яўляецца рашэннем задачы аднамернай мінімізацыі:
f (x (k) + ts (k)) -> min, t ОR1, (k = 0,1,2, ...),
і можа вызначацца, у прыватнасці, метадам сканавання.
Дэталёвая рэалізацыя агульнай схемы ў двухмернай выпадку R2 дае траекторый набліжэння да кропкі х * метадам покоординатного спуску, якая складаецца з звёнаў ламанай, якія вядуць у пункту х (k), х ~ (k), x (k + 1) (k = 0, 1, 2,) (мал.2). Пры k = 0, зыходзячы з пачатковай кропкі х (0) = (x1 (0), x2 (0)), знаходзяць кропку х ~ (0) = (x1 ~ (0), x2 (0)), мінімуму функцыі адной зменнай f (x1, x2 (0)); пры гэтым f (x ~ (0)) <= f (x (0)). Затым знаходзяць кропку мінімуму x (1) функцыі f (x1 ~ (0), x2) па другой каардынаце. Далей робяць наступны крок вылічэнняў пры k = 1. Мяркуюць, што зыходнай кропкай разліку з'яўляецца х (1). Фіксуючы другую каардынату кропкі х (1), знаходзяць кропку мінімуму х ~ (1) = (x1 ~ (1), x2 (1)), функцыі f (x1, x2 (1)) адной зменнай x (1); пры гэтым f (x ~ (1)) <= f (x (1)) <= f (x (0)). Кропку х (2) атрымліваюць, мінімізуючы мэтавую функцыю f (x1 ~ (1), x2), зноў па коорданате х2, фіксуючы каардынату x1 ~ (1), кропкі x (1), і г.д.
Умовай спынення вылічальнай працэдуры пры дасягненні зададзенай дакладнасці e можа служыць няроўнасць
|| x (k + 1) - x (k) || <e (4)
Блок-схема пошуку мінімуму функцыі дзвюх зменных метадам покоординатного спуску.

Метад градыентнага спуску.
Разгледзім функцыю f, лічачы для пэўнасці, што яна залежыць ад трох зменных x, y, z. Вылічым яе прыватныя вытворныя дf / дх, дf / ду, дf / дz і ўтвараем з іх дапамогай вектар, які называюць градыентам функцыі:
grad f (x, у, z) = дf (х, у, z) / дх * i + дf (x, у, z) / ду * j + дf (x, y, z) / дг * k.
Тут i, j, k - адзінкавыя вектары, паралельныя каардынатных восях. Прыватныя вытворныя характарызуюць змена функцыі f па кожнай незалежнай зменнай у паасобку. Адукаваны з іх дапамогай вектар градыенту дае агульнае ўяўленне аб паводзінах функцыі ў наваколлі кропкі (х, у, z). Кірунак гэтага вэктару з'яўляецца напрамкам найбольш хуткага ўзрастання функцыі ў дадзенай кропцы. Супрацьлеглае яму кірунак, якое часта называюць антиградиентным, уяўляе сабой напрамак найбольш хуткага змяншэння функцыі. модуль градыенту
(| grad (х, у, z) |) 2 = (дf / дх (х, у, z)) 2 + (дf / ду (x, у, z)) 2+ (дf / дг (x, y , z)) 2
вызначае хуткасць ўзрастання і змяншэння функцыі ў напрамку градыенту і антиградиента. Для ўсіх астатніх кірункаў хуткасць змены функцыі ў кропцы (х, у, z) менш модуля градыенту. Пры пераходзе ад адной кропкі да іншай як кірунак градыенту, так і яго модуль, наогул кажучы, змяняюцца. Паняцце градыенту натуральным чынам пераносіцца на функцыі любога ліку зменных. Пяройдзем да апісання метаду градыентнага спуску. Асноўная яго ідэя складаецца ў тым, каб рухацца да мінімуму ў напрамку найбольш хуткага змяншэння функцыі, якое вызначаецца антиградиентом. Гэтая ідэя рэалізуецца наступным чынам. Абярэм якім-небудзь спосабам пачатковую кропку, вылічым ў ёй градыент разгляданай функцыі і зробім невялікі крок у зваротным, антиградиентном кірунку. У выніку мы прыйдзем у кропку, у якой значэнне функцыі будзе менш першапачатковага. У новай кропцы паўторым працэдуру: зноў вылічым градыент функцыі і зробім крок у адваротным напрамку. Працягваючы гэты працэс, мы будзем рухацца ў бок змяншэння функцыі. Спецыяльны выбар кірунку руху на кожным кроку дазваляе спадзявацца на тое, што ў дадзеным выпадку набліжэнне да найменшага значэння функцыі будзе больш хуткім, чым у метадзе покоординатного спуску. Метад градыентнага спуску патрабуе вылічэнні градыенту мэтавай функцыі на кожным кроку. Калі яна зададзена аналітычна, то гэта, як правіла, не праблема: для прыватных вытворных, якія вызначаюць градыент, можна атрымаць відавочныя формулы. У адваротным выпадку прыватныя вытворныя ў патрэбных кропках даводзіцца вылічаць набліжана, замяняючы іх адпаведнымі рознасныя адносінамі:
дх ~ (дf ~ f (x1, ..., xi + Dxi, ..., xn) - f (x1, ..., xi, ..., xn)) / D xi
Адзначым, што пры такіх разліках Dxi, нельга браць занадта малым, а значэнні функцыі трэба вылічаць з досыць высокай ступенню дакладнасці, інакш пры вылічэнні рознасці Df (x1, ..., xi + Dxi, ..., xn) - f (x1 , ..., xi, ..., xn) будзе дапушчана вялікая памылка. На мал. 3 намаляваныя лініі ўзроўню той жа функцыі дзвюх зменных u = f (х, у), што і на мал. 2, і прыведзена траекторыя пошуку яе мінімуму з дапамогай метаду градыентнага спуску.
Параўнанне мал. 2 і 3 паказвае, наколькі больш эфектыўным з'яўляецца метад градыентнага спуску.

Мал. 3. Пошук найменшага значэння функцыі метадам градыентнага спуску
Метад найхутчэйшага градыентнага спуску.
Вылічэнне градыенту на кожным кроку, якое дазваляе ўвесь час рухацца ў напрамку найбольш хуткага змяншэння мэтавай функцыі, можа ў той жа час запаволіць вылічальны працэс. Справа ў тым, што падлік градыенту - звычайна значна больш складаная аперацыя, чым падлік самой функцыі. Таму часта карыстаюцца мадыфікацыяй градыентнага метаду, якая атрымала назву метаду найхутчэйшага спуску.
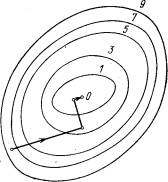
Мал.4 Пошук найменшага значэння функцыі метадам найхутчэйшага спуску
Згодна з гэтым метадзе пасля вылічэнні ў пачатковай кропцы градыенту функцыі робяць у кірунку антиградиента не маленькі крок, а рухаюцца да таго часу, пакуль функцыя меншае. Дасягнуўшы пункту мінімуму на абраным кірунку, зноў вылічаюць градыент функцыі і паўтараюць апісаную працэдуру. Пры гэтым градыент вылічаецца значна радзей, толькі пры змене напрамкаў руху.
На мал. 4 паказаная траекторыя пошуку найменшага значэння мэтавай функцыі па метадзе найхутчэйшага спуску. . Функцыя абраная тая ж, што і на мал.2, 3. Хоць траекторыя вядзе да мэты не так хутка, як на мал. 3, эканомія машыннага часу за кошт больш рэдкага вылічэнні градыенту можа быць вельмі істотнай.
/ Крыніца інфармацыі: http://school-sector.relarn.ru/dckt/projects/optim/index.htm
прыклад:
спампаваць файл MathCad (Для аптымізацыі іншай функцыі трэба памяняць толькі формулу f (x1, x2): = (x1 + 1) 4+ (x2 + 1) 4+ (x1 + 1) 2+ (x2 + 1) 2 на тую якая Вам патрэбна; адказ глядзіце ў канцы дакумента.)



