Наша команда-партнер Artmisto
Obecnie, w praktyce organizacji projektowych, potraktowano szeroko rozpowszechnione uproszczone metody obliczania sieci ogrzewania wodnego, w których układ sieci i rozmieszczenie podstacji wspomagających i dławiących są przedstawione bez obliczeń optymalizacyjnych, a średnice rur są określone przez standardową wartość określonej liniowej straty ciśnienia - do 78,5 Pa / m (do 8 mm wody. St / m), podjęte na stałe w kierunku głównej autostrady. W tym przypadku lokalizacje i parametry podstacji wspomagających i dławiących są wybierane na podstawie intuicji inżynierskiej i doświadczenia projektanta. Metody te oparte są na fundamentalnych badaniach metod analitycznych optymalizacji parametrów sieci cieplnych wykonanych przez prof. B. L. Shifrinson już w latach 30. [76], a następnie rozwinął się w pracach innych inżynierów energetycznych [14, 28, 43, 60]; zapewnili, że podczas projektowania sieci cieplnych we wczesnych etapach rozwoju systemów ciepłowniczych podjęto wystarczająco optymalne decyzje, gdy systemy te były stosunkowo małe. Takie uproszczone metody obliczania sieci cieplnych mogą być również stosowane dzisiaj w projektowaniu stosunkowo małych systemów dostarczania ciepła o małej długości sieci cieplnych. Jednocześnie nie mogli w pełni wykorzystać teoretycznych zasad tych badań ze względu na ograniczone możliwości ręcznego liczenia. Często, porównując kombinowane i oddzielne schematy zasilania miast i centrów przemysłowych, koszty sieci cieplnych są określane na podstawie ogólnych zależności inwestycji w sieci cieplne od zintegrowanych wskaźników gęstości ciepła w regionach utrwalających ciepło. Przy stosowaniu takich metod, stopniowy wzrost obciążeń cieplnych konsumentów w latach okresu rozliczeniowego, nie uwzględnia się istniejących odcinków sieci, a średnice odcinków sieci ciepłowniczych nie są optymalizowane, biorąc pod uwagę ograniczenia techniczne dotyczące ciśnienia w węzłach sieci, różne konkretne inwestycje kapitałowe dla jego sekcji, co może prowadzić do znaczące błędy i błędy. Wykorzystanie komputerów stwarza ogromne możliwości tworzenia nowych, bardziej zaawansowanych i dokładnych metod optymalizacji rozwoju sieci grzewczych [26, 41, 42, 50, 65].
Zadanie optymalizacji sieci cieplnych można rozwiązać bez uwzględnienia i uwzględnienia stopniowego wzrostu obciążeń cieplnych w latach okresu rozliczeniowego. Jeśli czynnik dynamiki nie jest brany pod uwagę, stwierdzenie problemu można sformułować w następujący sposób. Określone: szacowane zużycie wody u konsumentów; długość odcinków i konfiguracja sieci cieplnej; zakres dopuszczalnych wartości określonego spadku ciśnienia w głównej linii; żywotność istniejącej sieci cieplnej i średnice jej poszczególnych sekcji; skala standardów dla możliwych średnic sieci cieplnej; dopuszczalna jednorazowa presja na abonentów; techniczne ograniczenia ciśnienia w węzłach sieci. Wymagane jest określenie: optymalnych wartości średnic odcinków sieci; Liczba, lokalizacja i parametry podstacji wspomagających i przepustnic odpowiadających minimalnej wartości funkcji celu, która jest wykorzystywana jako obniżone koszty w sieci ciepłowniczej Wartości zawarte w kwocie inwestycji / Cf są obliczane według wzoru:
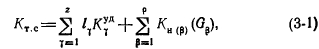

Optymalizacja parametrów sieci cieplnej, czyli znalezienie minimum funkcji obniżonego kosztu za pomocą modelowania matematycznego i komputera, może być przeprowadzona za pomocą następujących metod:
1) wyszukiwanie wystarczająco dużej liczby opcji z różnymi wartościami określonego spadku ciśnienia wzdłuż kierunku linii głównej pod warunkiem liniowego prawa spadku ciśnienia wzdłuż tego kierunku (metoda liniowa);
2) metoda oparta na wykorzystaniu programowania dynamicznego (metoda nieliniowa).
Ogólnie, matematyczne sformułowanie problemu optymalizacji sieci cieplnej za pomocą metody liniowej można zapisać w następujący sposób. Znajdź:

Liniowa metoda optymalizacji sieci cieplnej polega na całkowitym wyliczeniu określonych wartości określonego spadku ciśnienia (h) w głównej linii sieciowej, uznawanego za taki sam we wszystkich jego sekcjach, oraz w znalezieniu jego optymalnej wartości odpowiadającej minimalnej funkcji kryterium. W obliczeniach / r (PCT, potrzeba iteracji wszystkich swoich wartości (z danym krokiem) leżących w dozwolonym regionie jest spowodowana faktem, że zależność 3 = f (h) nie charakteryzuje się ścisłą monotonicznością gładką, tj. Mogą wystąpić lokalne minima. ich wygląd jest spowodowany dyskrecją średnic rur i rozmiarów konstrukcji budowlanych, a także obecnością działek w rozwijających się sieciach cieplnych, przy czym lokalne minima odpowiadają tym opcjom, w których istniejące działki nie są przesuwane. W wyniku obliczeń na komputerze możliwe jest uzyskanie nie jednego optymalnego wariantu, ale zestawu kilku wariantów, które nieznacznie różnią się od optymalnych przy obniżonych kosztach, co pozwala projektantowi wybrać opcję nie tylko przez formalne kryterium minimalnych obniżonych kosztów, ale także biorąc pod uwagę wymagania operacyjne, na przykład hydrauliczne stabilność i niezawodność.
Założenie liniowości prawa spadku ciśnienia wzdłuż głównej magistrali grzewczej upraszcza obliczanie sieci grzewczej i jednocześnie wprowadza błąd w wynikach jej optymalizacji. Na przykład metoda liniowa nie pozwala w pełni uwzględnić różnic w metodach układania rurociągów dla różnych części sieci. W przypadku optymalizacji rozwijającej się sieci z istniejącymi sekcjami, ta metoda nie pozwala uwzględnić ważnej cechy, która polega na tym, że dla nowych odcinków sieci optymalne wartości określonej straty ciśnienia są zwykle mniejsze niż dla istniejących. Tłumaczy to fakt, że w sieciach z istniejącymi obiektami udział kosztów transferu chłodziwa w całkowitym koszcie sieci grzewczej jest większy.
Nieliniowa metoda optymalizacji sieci cieplnych opiera się na podzieleniu głównego szkieletu sieci na oddzielne sekcje z optymalizacją sieci krok po kroku dla poszczególnych sekcji [26]. Dzięki tej metodzie, zamiast znaleźć minimum funkcji obniżonego kosztu w całej sieci, w zależności od średnic wszystkich sekcji, co wymaga rozwiązania złożonego układu równań, konsekwentnie znaleziono optymalne rozwiązania dla poszczególnych sekcji sieci.
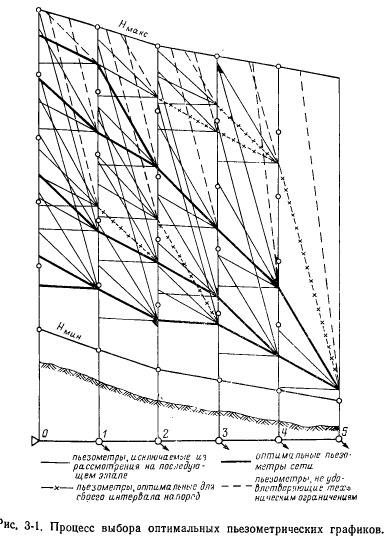
Podstawowe założenia metody programowania dynamicznego i kolejność rozwiązywania problemu w jego zastosowaniu omówiono powyżej na przykładzie optymalizacji składu i czasu uruchomienia urządzeń kogeneracyjnych. W tym przypadku proces krok po kroku jest budowany z uwzględnieniem specyfiki problemu optymalizacji sieci cieplnej. Podstawą (zmienna fazowa) jest głowa, która jest podzielona na szereg wartości (w określonych granicach - od minimum do maksymalnej dopuszczalnej wartości) tworząc punkty sieci. Patrząc na opcje na każdym kroku i obliczając obniżone koszty dla danej i-tej głowy, I, wartość I jest dostosowywana do najbliższej standardowej średnicy. Proces optymalizacji krok po kroku, którego główna sekwencja zastosowania jest wyjaśniona przez konstrukcję z rys. 3-1 [26], zaczyna się od ostatniego segmentu y, ponieważ zakłada się, że ciśnienie na końcu sieci jest znane. Jednocześnie brane są pod uwagę wszystkie możliwe rozwiązania dla danego odcinka, które odpowiadają standardowym wartościom średnicy. Rozwiązania, dla których ciśnienie w początkowym węźle rozpatrywanej sekcji jest poza dopuszczalnym zakresem, nie są brane pod uwagę. Jeśli kilka wartości średnicy mieści się w jednym miejscu sieci, to według kryterium minimalnego obniżenia kosztów określa się optymalne rozwiązanie dla tego miejsca.
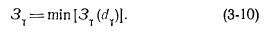
W następnym kroku w obliczeniach uwzględniane są dwie sekcje - ostatnia i ostatnia (y - 1), w tym przypadku rozważane są możliwe rozwiązania dla miejsca (y - 1), które są kontynuacją optymalnych rozwiązań dla każdego węzła sieci uzyskanego w poprzednim kroku. Jeśli kilka rozwiązań mieści się w jednym miejscu sieci (prawdopodobieństwo tego jest znacznie większe niż w pierwszym kroku), wówczas optymalne rozwiązanie jest określane dla dwóch segmentów yi (y - 1):
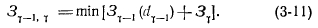
Dodając do już rozważanego następnego (w kolejności lokalizacji) odcinka sieci grzewczej, proces optymalizacji jest powtarzany. Zatem na każdym etapie średnica początkowego segmentu sieci, która ma zostać zoptymalizowana, jest przyjmowana jako zmienna fazowa, dla której dokonywana jest optymalizacja. Jednocześnie liczba możliwych rozwiązań ustalonych dla danego kroku, przy przechodzeniu do następnego etapu (sekcji sieci grzewczej), jest zwykle mniejsza niż liczba miejsc kratowych, x. e. liczba wartości zadanych w sieci, która pozostaje taka sama w całym procesie optymalizacji krok po kroku. Ostateczna decyzja dotycząca całej sieci jest wybierana po zakończeniu tego procesu i porównaniu między sobą przez wartość całkowitych obniżonych kosztów wszystkich otrzymanych „trajektorii”, tj. Możliwych opcji, których liczba nie przekracza określonej liczby wartości czołowych w sieci. Ważność zastosowania programowania dynamicznego do optymalizacji sieci cieplnych przedstawiono w [26].
Nieliniowa metoda optymalizacji pozwala uwzględnić charakterystykę techniczną i kosztową każdego segmentu sieci, wybrać optymalne miejsca budowy i parametry podstacji pompowych, zoptymalizować rozwijające się sieci z istniejącymi sekcjami. Ta metoda, oparta na optymalizacji krok po kroku, ma zastosowanie do rozległych sieci z pojedynczymi i wieloma źródłami ciepła, ale może być wykorzystana do optymalizacji sieci pierścieniowych, ponieważ w tych sieciach, w zależności od średnicy, jedna z sekcji zmienia zużycie wody przez inne części sieci. Zarówno metody nieliniowej, jak i liniowej optymalizacji można zastosować w sieciach pierścieniowych tylko w przypadkach, w których sieć pierścieniowa może zostać przekształcona na promieniową iz błędem dopuszczalnym, a rozkład przepływu jest z góry określony.
Aby ocenić porównawczą skuteczność różnych metod optymalizacji, wykonano obliczenia sieci cieplnej różnych konfiguracji przy użyciu trzech metod: metody obecnie szeroko stosowanej w praktyce projektowej i opartej na stosowaniu norm i liczenia ręcznego (a); metoda optymalizacji oparta na założeniu celowości zmiany ciśnienia w linii głównej zgodnie z prawem liniowym („metoda liniowa”) podczas wykonywania obliczeń na komputerze (b); metoda optymalizacji oparta na programowaniu dynamicznym („metoda nieliniowa”) podczas wykonywania obliczeń na komputerze (c).
Khrilev, L.S., Smirnov, I.A., Optymalizacja systemów ciepłowniczych i ciepłownictwa, Ed. E. Ya. Sokolova - M.: Energy, 1978.




