Как PageRank действительно работает: понимание Google

Наша команда-партнер Artmisto

Этим летом, находясь в отпуске, учитель математики подошел ко мне в ресторане и попросил объяснить формулу PageRank на моей футболке, которая действительно является ключом к пониманию алгоритмов Google. Это заставило меня задуматься и создать лучшее объяснение PageRank, которое я могу найти. Надеюсь, лучше, чем другие, которые я видел на Youtube.

Конечно, будучи Гиком, я носил матричную форму алгоритма PageRank. Алгоритм, благодаря которому Ларри Пейдж и Сергей Брин стали двумя самыми богатыми и влиятельными людьми в мире. Это математика, которая построила Google.

Чтение этого буквально говорит;

«PageRank страницы в этой итерации равен 1 минус коэффициент демпфирования, ПЛЮС… за каждую ссылку на страницу (кроме ссылок на нее), добавьте рейтинг страницы этой страницы, деленный на количество исходящих ссылок на странице и уменьшается на коэффициент демпфирования. »

Легко ли?

Ну, может быть, для некоторых из вас. Но этот алгоритм является фундаментальным для понимания ссылок и, в частности, понимания, почему большинство ссылок ничего не значат или почти ничего. Когда вы овладеете алгоритмом Google, вы будете на несколько лет опережать других SEO-специалистов ... но я никогда не вижу, чтобы это было должным образом объяснено. Я гарантирую, что даже если вы знаете этот алгоритм наизнанку, вы увидите некоторые неожиданные результаты этой математики к концу этого поста, и вы никогда больше не будете использовать фразу «полномочия домена» перед клиентом (по крайней мере, в отношение к ссылкам).

Я не прошу никого здесь знать намного больше, чем простой Excel.

Я собираюсь начать с того, что покажу, как эта математика применима к этому представлению ОЧЕНЬ маленькой интернет-системы с 5 узлами. Затем мы рассмотрим совсем немного другую карту, которая имеет глубокие последствия для наших результатов.

Прежде чем мы начнем, возможно, взглянем на это и Угадай, какой узел имеет самый высокий PageRank (Голова линий головастиков - это «стрелки», показывающие направление ссылок).

Алгоритм PageRank называется итеративным алгоритмом. Мы начинаем с некоторых оценок, а затем постоянно совершенствуем наше понимание экосистемы, которую мы измеряем. Итак, как мы можем увидеть, как эта формула применима к этой экосистеме?

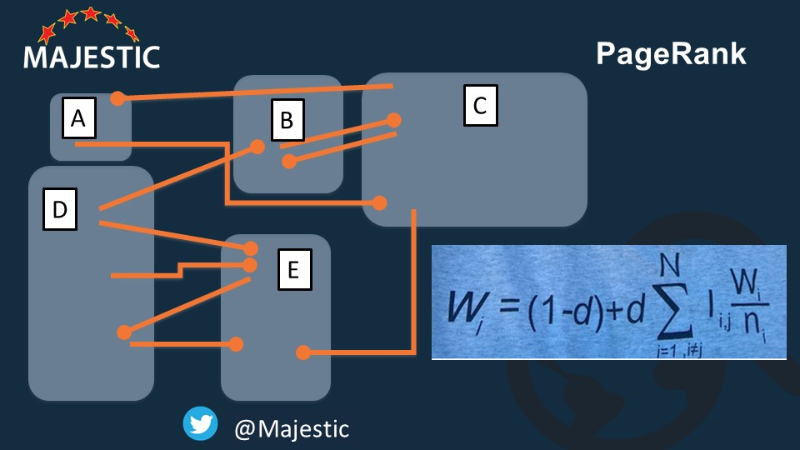
Во-первых, нам нужно создать матрицу… у нас есть узлы от A до E. Я пока назову их страницами, потому что это терминология, которую мы понимаем, но фанаты хардкора должны знать, что я имею в виду «узлы», так как это важно позже ,

1. Начальное значение (в данном случае) - количество фактических ссылок на каждый «узел». Большинство людей фактически устанавливают для этого значение 1, но есть две веские причины для использования количества ссылок. Во-первых, лучше начать с первого приближения, чем давать все одинаковое значение, поэтому алгоритм стабилизируется за меньшее число итераций, и поэтому очень полезно проверить мою электронную таблицу за секунду… поэтому узел A имеет одну ссылку (со страницы C)
2. Теперь давайте наметим все пробелы в матрице ... Начиная с каждой страницы нельзя ссылаться на себя (ОК ... может ... но не в алгоритме Google)
3. Узел А ТОЛЬКО ссылки на С
4. Узел B ТОЛЬКО ссылки на C
5. Узел C к A, B & E
6. D - Ссылки на B и 3 раза на E! Вы считаете это один или три раза? Я собираюсь посчитать это ОДНАЖДЫ прямо сейчас, но мы вернемся к этой странности позже.
7. E только ссылки на D

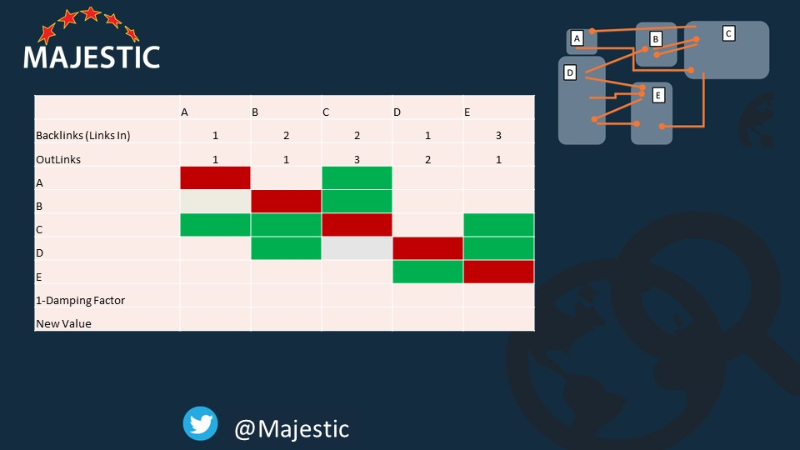
Так вот сетка. Здесь мы можем проверить несколько вещей… 8 зеленых прямоугольников = количество ссылок в нашем алгоритме (если мы только посчитали 3 ссылки от D до E один раз).

Кроме того - обратите внимание, что большая часть этой сетки красного цвета ... большинство страниц в Интернете не ссылаются друг на друга.

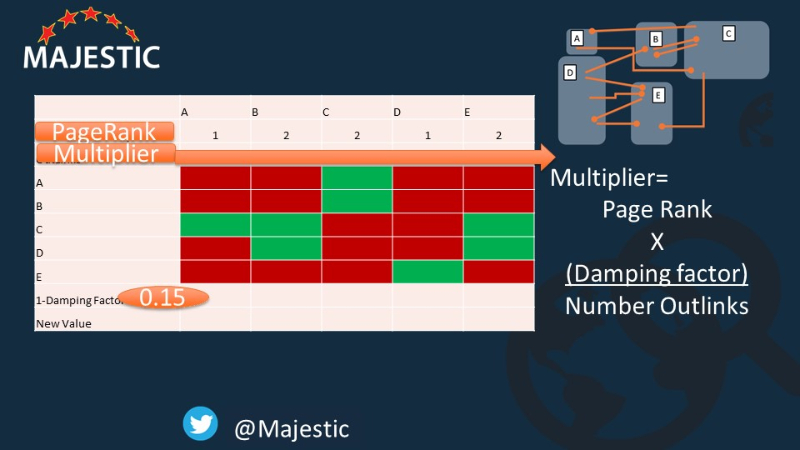
Это упрощение этой формулы. Это не слишком страшно сейчас, не так ли? Так что теперь мы можем добавить множитель для каждого столбца. Это значение, которое каждая ссылка будет передавать на страницы, на которые она ссылается.

Так, например, страница А имеет PR 1, умноженное на 0,85 и разделенное на одну исходящую ссылку. Таким образом, множитель 0,85

На странице C PR = 2. Множитель 2 X 0,85, разделенный на три исходящие ссылки. Это означает, что каждый из них дает 0,566666 баллов.

(Эта презентация не будет идти в случае, когда Outlinks равен нулю.)

Итак, теперь мы идем по зеленым коробкам, заполняя зеленые коробки. Так…

Страница A дает одну ссылку на страницу C ... каждая ссылка, которую она дает, имеет значение 0,85 ... поэтому мы помещаем 0,85 в это поле.

Страница C ссылается на ТРИ страницы, давая каждому по 0,5666667…. И так до тех пор, пока зеленые боуи не заполнятся.

Теперь ... если вы помните, мы убрали коэффициент демпфирования до того, как начали, поэтому нам нужно добавить коэффициент демпфирования обратно на каждую страницу. Это означает, что общее количество PageRank останется стабильным.

Затем мы складываем столбцы, чтобы найти новые значения PageRank для каждой страницы! Вот завершенная сетка:

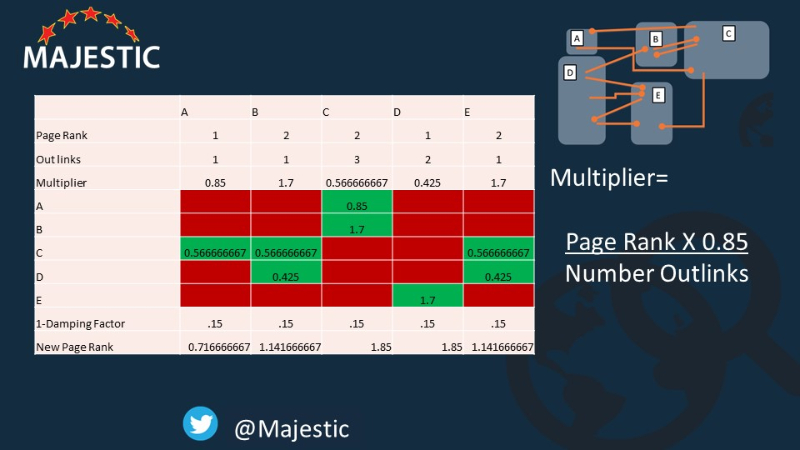
[РЕДАКТИРОВАТЬ 7 марта 2019 года: благодаря Пабло Родригес Сентено для указания на столбец C следует добавить до 2,7, а не 1,85 в таблице выше. Хорошее место!]

Теперь это все, что есть в алгоритме PageRank, но я сказал, что он итеративный. Поэтому вам нужно делать это снова и снова, чтобы получить реальный PageRank для каждой страницы. Поэтому я вырезал и вставлял значения обратно в начальные значения, чтобы получить следующую итерацию. На мои ящики уже есть ссылки, поэтому следующая итерация выполняется мгновенно ...

Если вы хотите посмотреть мою таблицу Excel, кстати, вот что нужно сделать.

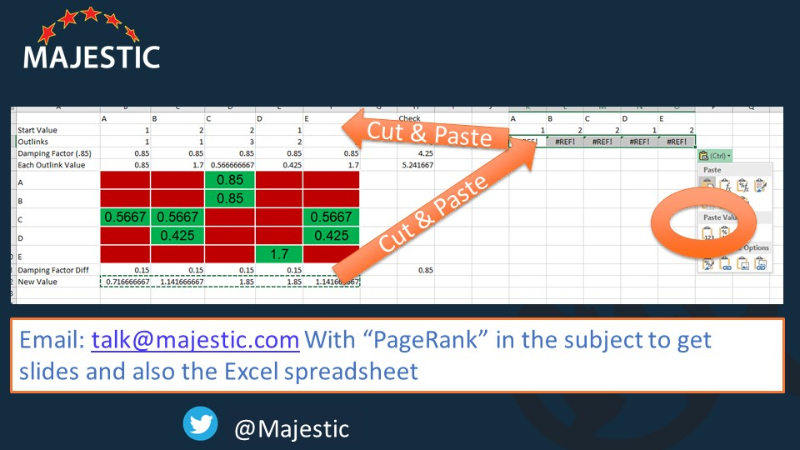
... Я беру цифры внизу ...

И поместите их в верхнюю часть ... давая мне новые цифры внизу, которые я ...

Вырежьте и вставьте в вершину снова, чтобы получить третью итерацию ... и снова и снова.

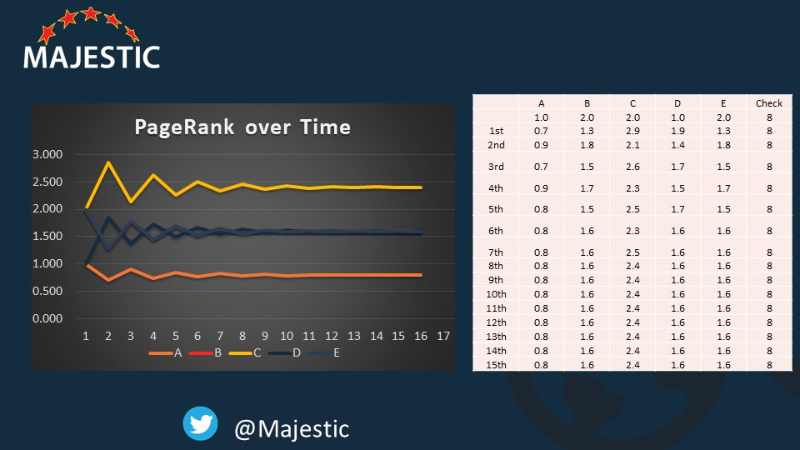
Это то, что происходит с числами после 15 итераций ... Посмотрите, как все 5 узлов стабилизируются на одинаковых числах. Кстати, если бы мы начинали со всех страниц, равными 1, то, что большинство людей говорят вам, потребовалось бы гораздо больше итераций, чтобы получить стабильный набор чисел (и на самом деле - в этой модели - не будет стабилизировались вообще)

Теперь мы сделали математику, мы можем увидеть, какая страница является самой важной в нашем Интернете.

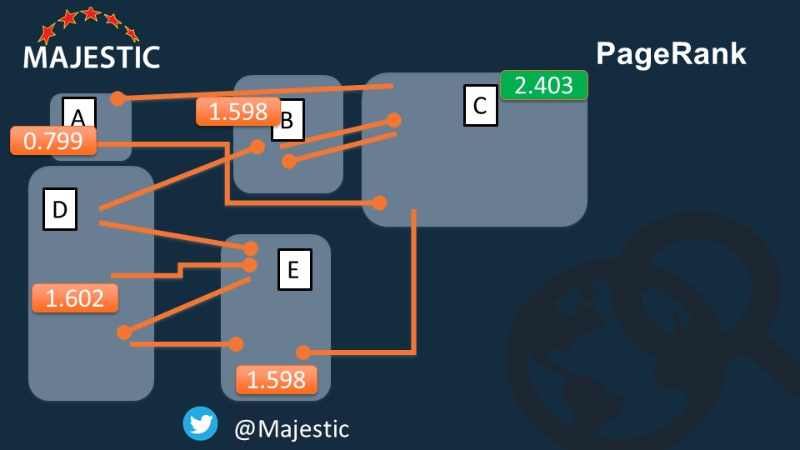
Это был тот, который вы угадали? Хорошо ли вы сказали «да» или «нет»… Пришло время раскрыть более широкую историю.

Вы помните, я сказал «узлы» вместо «страниц»? Это потому, что это делало PageRank с наименьшим общим знаменателем, который у меня был… 5 узлов. Но что, если это на самом деле домены, а не страницы? ... теперь я добавлю страницы для каждого домена и начну заново ...

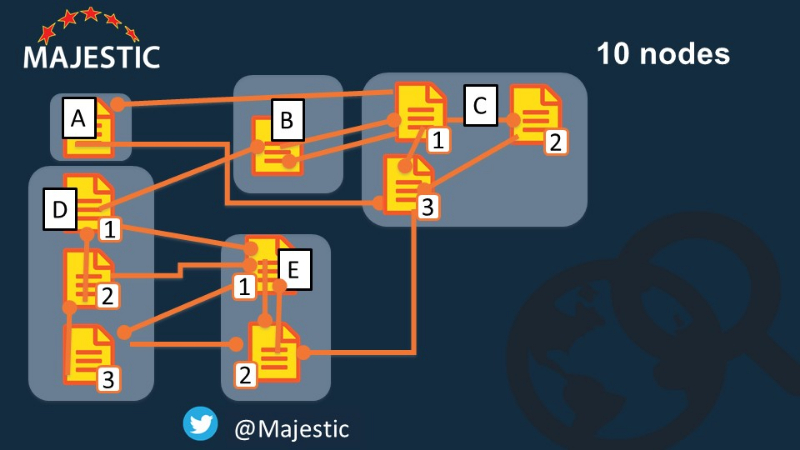
Так что теперь у нас есть 10 узлов, а не 5 ... и ВАЖНО, у нас теперь есть внутренняя связь ...

Как вы думаете, где сила будет лежать в этой версии Интернета?

Достаточно ли я безумен, чтобы снова выполнить все расчеты? О да ...

... и вот фактические оценки для каждой страницы.

Страной-победителем является Узел E1.

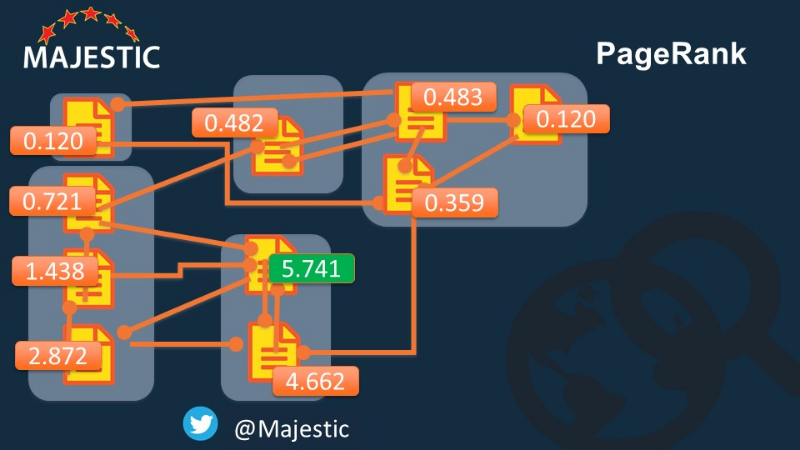
Домен-победитель был сайтом C в 5-узловой модели, поэтому, если бы вы использовали моделирование на уровне домена, вы бы надеялись на ссылки со страниц, которые среди САМЫХ худших на уровне страниц.

Внутренние ссылки на сайте, который вы не можете контролировать, сильно влияют на PageRank ваших собственных страниц!

PageRank выполнялся НИКОГДА только на уровне страницы ... Majestic выполняет наши расчеты на верхнем уровне, уровне субдомена и уровне страницы - и в стремлении показать нашим клиентам большее количество ссылок, мы сначала используем TLD, как и наши конкуренты ... но это уровень страницы, который имеет значение.

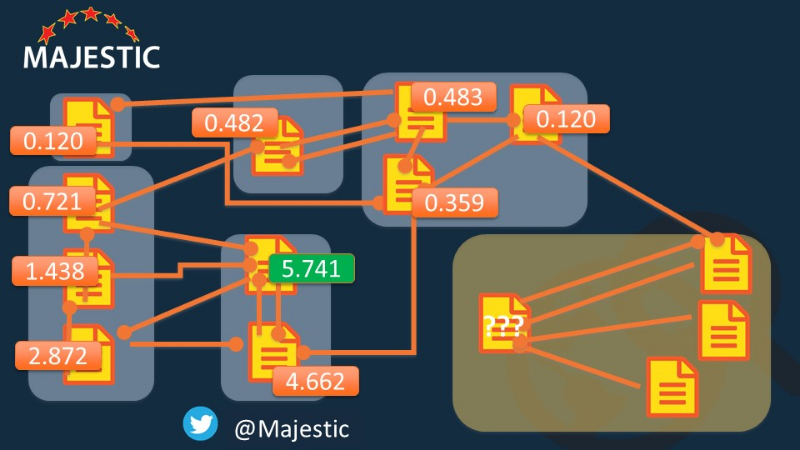
Если вы создаете новый сайт и используете только Domain Authority для создания ссылок, вы можете легко получить ссылку с самой худшей из возможных страниц, даже если она была из лучшего домена, из-за ВНУТРЕННИХ ССЫЛК других веб-страниц! Как же вы сможете увидеть силу ссылки, если она зависит от внутренних ссылок на совершенно другом веб-сайте ?!

Второе наблюдение заключается в том, что данные не обязательно должны быть полными, но они лучше всего работают с универсальным набором данных.

Еще в 2014 году один из наших исследователей написал этот пост в блоге после того, как исследование с использованием алгоритма PageRank ТОЛЬКО в Википедии показало Карл Линней как более влиятельный, чем Иисус или Гитл р.

Поток цитирования Majestic, как прокси-сервер PageRank, мог бы сказать исследователю другой, более вероятный результат, поскольку наши данные используют больший раздел Интернета.

Следующая странность заключается в том, что большинство страниц имеют любой PageRank вообще! Три верхние страницы в этой 10-узловой модели составляют 75-80% всего PageRank системы.

«Ссылка считается начальной оценкой для PageRank отстой в качестве показателя»

Следующая странность - первоначальная догадка ... об использовании количества ссылок в качестве начальной оценки для PageRank отстой в качестве метрики. На этом графике PageRank каждой страницы представлен в виде области. Когда мы начинали, страница C3 была нашей лучшей догадкой о самом высоком PageRank. Но посмотрите, сколько любви она теряет к концу моделирования.

«PageRank не пропускает»

В обеих версиях моей модели я использовал общее количество моих начальных оценок, чтобы проверить, что моя математика не работает на юг. После каждой итерации общий Pagerank остается неизменным. Это означает, что PageRank не протекает! Переадресация 301 не может просто удалить PageRank, иначе алгоритм может не остаться стабильным. Аналогично, страницы с нулевыми исходящими ссылками нельзя «исправить», разделив их на что-то отличное от нуля. Они должны быть исправлены, но не разбавляя общий PageRank. Я могу, возможно, взглянуть на эти случаи более подробно, если есть спрос.

Интернет большой

Я хотел бы оставить вас с этими мыслями. Я показал вам, как это работает в мире размером 10 страниц.

10 страниц X 10 вычислений (хотя многие умножены на ноль), а затем 15 итераций - 1500 бит математики.

Majestic выполняет аналогичные (но разные) вычисления для 500 миллиардов URL-адресов в день для нашего индекса Fresh и в настоящее время для исторического индекса 1,8 миллиарда страниц в месяц.

Прокси-серверы PageRank трудны для построения!

... что является лишь одной из причин, почему Google до сих пор не может отпустить ... Это твит от Google Gary.

Наконец, PageRank не касается ранжирования, потому что Pure Pagerank НЕ учитывает контекст. Так что будьте очень осторожны в использовании метрик страницы, которые основаны на видимости поиска. Поток цитирования Majestic представляет собой наиболее чистую корреляцию с доступным в настоящее время PageRank, хотя алгоритм немного отличается.

PageRank является товарным знаком Google. Алгоритм защищен (в США) патентом US6285999 и присвоен Стэнфордскому университету. Хотя формула Majestic тесно связана с тестами PageRank, в ней есть некоторые уникальные отличия, которые мы не публикуем.

назад