Наша команда-партнер Artmisto
Визначення. Нехай потрібно вирішити задачу (2): f (x) -> min, х Про Rn (2) У двовимірному пространтсва R2 вирішення такого завдання можна дати геометричну ілюстрацію. Нехай точка х = (х1, х2) лежить на площині Ох1х2. Введемо третю координату х3 так, щоб вісь координат Ох3 була перпендикулярна площині Ох1х2 (рис.1). Рівняння х3 = f (х1, х2) відповідає поверхню в тривимірному просторі.
Якщо функція f (х) досягає локального мінімуму в точці х * Про R2, то поверхня в деякій околиці точки х * має форму чаші (рис.1).

рис.1
Нагадаємо, що лініями рівня функції f (х1, х2) називають сімейство ліній площині R2, на яких функція приймає постійне значення. Неявним рівнянням лінії рівня є рівняння f (x1, x2) = C. Якщо функція f (x) має в R2 єдину точку локального мінімуму
х * (х * 1, х * 2), то така функція називається мономодальні. Взаємне розташування її ліній рівня має вигляд, зображений на рис.2.
Мультимодальні називаються функції, які мають більше одного екстремуму. Така, наприклад, функція Гіммельблау
F (x) = (x12 + x2-11) 2+ (x1 + x22-7) 2,
має чотири ізольовані точки мінімуму. На рис.3 схематично зображено лінії рівня цієї функції.

рис.2
Щоб знайти точку х * локального мінімуму функції f (х), складають послідовність точок (наближень до рішення) {х (k)} (k = 0,1, ...), що сходиться до точки х *
(K = 0,1, ...), що сходиться до точки х *.
Послідовність значень функції f (х (k)) повинна бути монотонно спадної і обмеженою знизу:
f (x (0))> = f (x (1))> =. . . > = F (x (k))> =. . . > = F (x (*)).
Геометричний образ рішення задачі (2) для випадку двох змінних нагадує спуск на дно чаші. Це мотивує назви методів вирішення задачі (2) - «методи спуску».
Для різних методів спуску спочатку вибирають початкову точку послідовності х (0). Подальші наближення х (k) визначаються співвідношеннями
x (k + 1) = x (k) + t (k) S (k) (k = 0, 1, 2,...), (12)
Де S (k) - вектор напрямку спуску; скалярна величина t (k) я | вляется рішенням завдання одномірної мінімізації
f (x (k) + ts (k)) -> min, t Про R. (13)
Таким чином, завдання пошуку мінімуму функції кількох змінних зводиться до послідовності задач одновимірної мінімізації (13) по змінній t на відрізках n-мірного простору, що проходять через точки х (k) в напрямку векторів S (k).
Методи спуску розрізняються вибором вектора спуску і способом юшенія завдання одномірної мінімізації.
При вирішенні послідовності завдань (12) можна обмежитися методом сканування для пошуку мінімуму функції однієї переменюй. Вибравши довільно початкову точку х (0) і розмір начальюго кроку h по змінної t, в методі сканування можна отримати різні точки мінімуму мультимодальной функції.
Якщо функція f (x) мономодальні, то незалежно від вибору початкової точки траєкторія пошуку повинна привести до єдиної точки локального мінімуму цієї функції.
Переважна кількість реальних завдань оптимізації, що представляють практичний інтерес, є багатовимірними: в них цільова функція залежить від декількох аргументів, причому іноді їх число може бути дуже великим.
Згадаймо, наприклад, задачу про хімічному виробництві. Ми відзначили, що в ній цільова функція залежить від температури, і при певному її виборі продуктивність (вихід цікавить нас продукту) виявляється максимальною. Однак, поряд з температурою, продуктивність залежить також від тиску, співвідношення між концентраціями вводиться сировини, каталізаторів і ряду інших чинників. Таким чином, завдання вибору найкращих умов хімічного виробництва - це типова багатовимірна задача оптимізації. Математична постановка "таких завдань аналогічна їх постановці в одновимірному випадку: шукається найменше (найбільше) значення цільової функції, заданої на деякій множині Е можливих значень її аргументів. У разі, коли целевля функція неперервна, а безліч Е є замкнутої обмеженою областю, залишається справедливою теорема Вейєрштрасса. Тим самим виділяється клас задач оптимізації, для яких гарантовано існування рішення. надалі ми завжди будемо припускати, не обумовлюючи цього особливо, що все розглядається як до Перші завдання належать цього класу. Як і в одновимірному випадку, характер завдання і відповідно можливі методи вирішення істотно залежать від тієї інформації про цільової функції, яка нам доступна в процесі її дослідження. В одних випадках цільова функція задається аналітичною формулою, будучи при цьому диференціюється функцією . Тоді можна обчислити її приватні похідні, отримати явний вираз для градієнта, що визначає в визначального в кожній точці, напрямки зростання та спадання функції,

Мал. 1.
Побудова сітки з кроком h і вибір "пробних" точок у вузлах сітки для наближеного визначення найменшого значення функції двох змінних. і використовувати цю інформацію для вирішення завдання. В інших випадках ніякої формули для цільової функції немає, а є лише можливість визначити її значення в будь-якій точці розглянутої області (за допомогою розрахунків, в результаті експерименту і т. Д.). У таких завданнях в процесі рішення ми фактично можемо знайти значення цільової функції лише в кінцевому числі точок, і з цієї інформації потрібно приблизно встановити її найменше значення для всієї області. Багатовимірні завдання, природно, є більш складними і трудомісткими, ніж одномірні, причому зазвичай труднощі при їх вирішенні зростають при збільшенні розмірності. Для того щоб ви краще відчули це, візьмемо найпростіший по своїй ідеї наближений метод пошуку найменшого значення функції, який вже обговорювалося для одновимірних задач в. Покриємо розглянуту область сіткою з кроком h (рис. 1) і визначимо значення функції в її вузлах. Порівнюючи отримані числа між собою, знайдемо серед них найменше і приймемо його наближено за найменше значення функції для всієї області. Як ми вже говорили вище, даний метод використовується для вирішення одновимірних задач. Іноді він застосовується також для вирішення двовимірних, рідше тривимірних задач. Однак для задач більшої розмірності він практично непридатний через занадто великого часу, необхідного для проведення розрахунків. Дійсно, припустимо, що цільова функція залежить від п'яти змінних, а область визначення є пятімерном кубом, кожну сторону якого при побудові сітки ми ділимо на 40 частин. Тоді загальне число вузлів сітки дорівнюватиме 415 ~ 108. Нехай обчислення значення функції в одній точці вимагає 1000 арифметичних операцій (це трохи для функції п'яти змінних). В такому випадку, загальне число операцій складе 1011. Якщо в нашому розпорядженні є ЕОМ з швидкодією 1 млн. Операцій в секунду, то для вирішення завдання за допомогою даного методу буде потрібно 105 секунд, що перевищує добу безперервної роботи. Додавання ще однієї незалежної змінної збільшить цей час в 40 разів. Проведена оцінка показує, що для великих завдань оптимізації метод суцільного перебору непридатний. Іноді суцільний перебір замінюють випадковим пошуком. В цьому випадку точки сітки проглядаються не підряд, а у випадковому порядку. В результаті пошук найменшого значення цільової функції істотно прискорюється, але втрачає свою надійність.
Метод покоордінатного спуску.
Нехай потрібно знайти найменше значення цільової функції u = f (M) = f (x 1, x 2,..., Xn). Тут через М позначена точка n-мірного простору з координатами x 1, x 2,. . . , xn: M = (x 1, x 2,..., xn). Виберемо яку-небудь початкову точку М 0 = (x 10, x 20,..., Xn0) і розглянемо функцію f при фіксованих значеннях всіх змінних, крім першої: f (x 1, x 20, x 30,..., xn0). Тоді вона перетвориться в функцію однієї змінної x 1. Змінюючи цю змінну, будемо рухатися від початкової точки x 1 = x 10 в сторону зменшення функції, поки не дійдемо до її мінімуму при x 1 = x 11, після якого вона починає зростати. Крапку з координатами (x 11, x 20, x 30,..., Xn0) позначимо через М 1, при цьому f (M0)> = f (M 1). Фіксуємо тепер змінні: x 1 = x 11, x 3 = x 30,. . . , xn = xn0 і розглянемо функцію f як функцію однієї змінної x 2: f (x 11, x 22, x 30..., xn0). Змінюючи x 2, будемо знову рухатися від початкового значення x2 = x20 в сторону зменшення функції, поки не дійдемо до мінімуму при x2 = x21 .Точку з координатами {x 11, x 21, x 30. . . xn0} позначимо через М 2, при цьому f (M1)> = f (M 2).
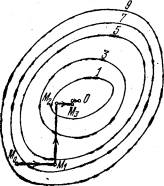
Мал. 2. Пошук найменшого значення функції методом покоордінатного спуску.
Проведемо таку ж мінімізацію цільової функції по змінним x 3, x 4,. . . , xn. Дійшовши до змінної xn, знову повернемося до x 1 і продовжимо процес. Ця процедура цілком виправдовує назву методу. З її допомогою ми побудуємо послідовність точок М 0, М 1, М 2,. . . , Якій відповідає монотонна послідовність значень функції f (M0)> = f (M 1)> = f (M 2)> = ... Обриваючи її на певному етапі k можна наближено прийняти значення функції f (Mk) за її найменше значення в даній області. Відзначимо, що даний метод зводить задачу пошуку найменшого значення функції кількох змінних до багаторазового вирішення одновимірних задач оптимізації. Якщо цільова функція f (x 1, x 2, ..., xn) задана явною формулою і є дифференцируемой, то ми можемо вичіслліть її приватні похідні і використовувати їх для визначення напрямку убування функцііпо кожної змінної і пошуку відповідних одновимірних мінімумів. В іншому випадку, коли явною формули для цільової функції немає, одномірні завдання слід вирішувати за допомогою одновимірних методів. На рис. 2 зображені лінії рівня деякою функції двох змінних u = f (х, у). Уздовж цих ліній функція зберігає постійні значення, рівні 1, 3, 5, 7, 9. Показана траєкторія пошуку її найменшого значення, яке досягається в точці О, за допомогою методу покоордінатного спуску. При цьому потрібно чітко розуміти, що малюнок є тільки для ілюстрації методу. Коли ми приступаємо до вирішення реальної завдання оптимізації, такого малюнка, що містить в собі готову відповідь, у нас, звичайно, немає. Нехай потрібно вирішити задачу (2):
f (x) -> min, х ОRn. (2)
У двовимірному пространтсва R2. Рішення завдання (2) методом покоордінатного спуску, інакше званого методом Гаусса - Зейделя, виробляють за такою загальною схемою.
Вибирають довільно початкову точку х (0) з області визначення функції f (х). Наближення х (k) визначаються співвідношеннями (3):
x (k + 1) = x (k) + t (k) S (k) (k = 0,1,2, ...),
де вектор напрямку спуску s (k) - це одиничний вектор, що збігається з яким-небудь координатним напрямком (наприклад, якщо S (k) паралельний х1, то S (k) = {1,0,0, ..., 0} , якщо він паралельний x2, то S (k) = {0, 1, 0,..., 0} і т.д.); величина t (k) є рішенням задачі одновимірної мінімізації:
f (x (k) + ts (k)) -> min, t ОR1, (k = 0,1,2, ...),
і може визначатися, зокрема, методом сканування.
Детальна реалізація загальної схеми в двовимірному випадку R2 дає траєкторій наближення до точки х * методом покоордінатного спуску, що складається з ланок ламаної, що з'єднують точки х (k), х ~ (k), x (k + 1) (k = 0, 1, 2,) (рис.2). При k = 0, виходячи з початкової точки х (0) = (x1 (0), x2 (0)), знаходять точку х ~ (0) = (x1 ~ (0), x2 (0)), мінімуму функції однієї змінної f (x1, x2 (0)); при цьому f (x ~ (0)) <= f (x (0)). Потім знаходять точку мінімуму x (1) функції f (x1 ~ (0), x2) по другій координаті. Далі роблять наступний крок обчислень при k = 1. Вважають, що вихідною точкою розрахунку є х (1). Фіксуючи другу координату точки х (1), знаходять точку мінімуму х ~ (1) = (x1 ~ (1), x2 (1)), функції f (x1, x2 (1)) однієї змінної x (1); при цьому f (x ~ (1)) <= f (x (1)) <= f (x (0)). Точку х (2) отримують, мінімізуючи цільову функцію f (x1 ~ (1), x2), знову по коорданате х2, фіксуючи координату x1 ~ (1), точки x (1), і т.д.
Умовою припинення обчислювальної процедури при досягненні заданої точності e може служити нерівність
|| x (k + 1) - x (k) || <e (4)
Блок-схема пошуку мінімуму функції двох змінних методом покоординатного спуску.
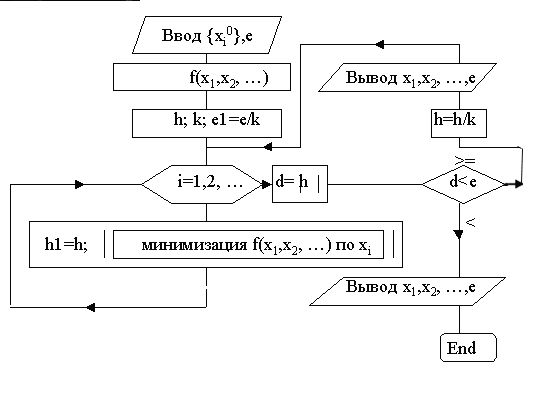
Метод градієнтного спуску.
Розглянемо функцію f, вважаючи для визначеності, що вона залежить від трьох змінних x, y, z. Обчислимо її приватні похідні Дf / дх, Дf / ду, Дf / дz і утворюємо з їх допомогою вектор, який називають градієнтом функції:
grad f (x, у, z) = Дf (х, у, z) / дх * i + Дf (x, у, z) / ду * j + Дf (x, y, z) / ДГ * k.
Тут i, j, k - одиничні вектори, паралельні координатним осях. Приватні похідні характеризують зміна функції f по кожній незалежної змінної окремо. Утворений з їх допомогою вектор градієнта дає загальне уявлення про поведінку функції в околі точки (х, у, z). Напрямок цього вектора є напрямом найбільш швидкого зростання функції в даній точці. Протилежне йому напрямок, яке часто називають антіградіентним, являє собою напрям найбільш швидкого спадання функції. модуль градієнта
(| grad (х, у, z) |) 2 = (Дf / дх (х, у, z)) 2 + (Дf / ду (x, у, z)) 2+ (Дf / ДГ (x, y , z)) 2
визначає швидкість зростання і спадання функції в напрямку градієнта і антіградіента. Для всіх інших напрямків швидкість зміни функції в точці (х, у, z) менше модуля градієнта. При переході від однієї точки до іншої як напрямок градієнта, так і його модуль, взагалі кажучи, міняються. Поняття градієнта природним чином переноситься на функції будь-якого числа змінних. Перейдемо до опису методу градієнтного спуску. Основна його ідея полягає в тому, щоб рухатися до мінімуму в напрямку найбільш швидкого спадання функції, яке визначається антіградіентом. Ця ідея реалізується в такий спосіб. Виберемо будь-яким способом початкову точку, обчислимо в ній градієнт даної функції і зробимо невеликий крок в зворотному, антіградіентном напрямку. В результаті ми прийдемо в точку, в якій значення функції буде менше початкового. У новій точці повторимо процедуру: знову обчислимо градієнт функції і зробимо крок в зворотному напрямку. Продовжуючи цей процес, ми будемо рухатися в сторону зменшення функції. Спеціальний вибір напрямку руху на кожному кроці дозволяє сподіватися на те, що в даному випадку наближення до найменшого значення функції буде швидшим, ніж в методі покоордінатного спуску. Метод градієнтного спуску вимагає обчислення градієнта цільової функції на кожному кроці. Якщо вона задана аналітично, то це, як правило, не проблема: для приватних похідних, що визначають градієнт, можна отримати явні формули. В іншому випадку приватні похідні в потрібних точках доводиться обчислювати наближено, замінюючи їх відповідними різницевими стосунками:
дх ~ (Дf ~ f (x1, ..., xi + Dxi, ..., xn) - f (x1, ..., xi, ..., xn)) / D xi
Відзначимо, що при таких розрахунках Dxi, не можна брати занадто малим, а значення функції потрібно обчислювати з досить високим ступенем точності, інакше при обчисленні різниці Df (x1, ..., xi + Dxi, ..., xn) - f (x1 , ..., xi, ..., xn) буде допущена велика помилка. На рис. 3 зображені лінії рівня тієї ж функції двох змінних u = f (х, у), що і на рис. 2, і приведена траєкторія пошуку її мінімуму за допомогою методу градієнтного спуску.
Порівняння рис. 2 і 3 показує, наскільки ефективнішим є метод градієнтного спуску.

Мал. 3. Пошук найменшого значення функції методом градієнтного спуску
Метод найшвидшого градієнтного спуску.
Обчислення градієнта на кожному кроці, що дозволяє увесь час рухатися в напрямку найбільш швидкого зменшення цільової функції, може в той же час сповільнити обчислювальний процес. Справа в тому, що підрахунок градієнта - зазвичай набагато більш складна операція, ніж підрахунок самої функції. Тому часто користуються модифікацією градиентного методу, що отримала назву методу найшвидшого спуску.

Рис.4 Пошук найменшого значення функції методом найшвидшого спуску
Відповідно до цього методу після обчислення в початковій точці градієнта функції роблять в напрямку антіградіента не маленький крок, а рухаються до тих пір, поки функція спадає. Досягнувши точки мінімуму на обраному напрямку, знову обчислюють градієнт функції і повторюють описану процедуру. При цьому градієнт обчислюється набагато рідше, тільки при зміні напрямків руху.
На рис. 4 показана траєкторія пошуку найменшого значення цільової функції за методом найшвидшого спуску. . Функція обрана та ж, що і на рис.2, 3. Хоча траєкторія веде до мети не так швидко, як на рис. 3, економія машинного часу за рахунок більш рідкісного обчислення градієнта може бути дуже істотною.
/джерело інформації: http://school-sector.relarn.ru/dckt/projects/optim/index.htm
приклад:
скачати файл MathCad (Для оптимізації іншої функції потрібно поміняти тільки формулу f (x1, x2): = (x1 + 1) 4 + (x2 + 1) 4 + (x1 + 1) 2+ (x2 + 1) 2 на ту яка Вам потрібна; відповідь дивіться в кінці документа.)



