Наша команда-партнер Artmisto
В даний час в практиці проектних організацій полікували широке поширення спрощені методи розрахунку водяних теплових мереж, при яких схема мережі і розміщення підкачуючих і дросселирующих підстанцій намічаються без оптимізаційних розрахунків, а діаметри трубопроводів визначаються за нормативним значенням питомої лінійної втрати тиску-до 78,5 Па / м (до 8 мм вод. ст / м), прийнятої постійної по напрямку головної магістралі. При цьому місця розташування і параметри підкачуючих і дросселирующих підстанцій вибираються на основі інженерної інтуїції і досвіду проектувальника. Ці методи базуються на фундаментальних дослідженнях аналітичних методів оптимізації параметрів теплових мереж, виконаних проф. Б. Л. Шіфрінсоном ще в 30-х роках [76] і згодом розвинених в працях інших енергетиків [14, 28, 43, 60]; вони забезпечували прийняття в достатній мірі оптимальних рішень при проектуванні теплових мереж на перших етапах розвитку систем централізованого теплопостачання, коли ці системи були порівняно невеликими. Такі спрощені методи розрахунку теплових мереж можуть застосовуватися і в даний час при проектуванні порівняно дрібних систем теплопостачання з незначною протяжністю теплових мереж. У той же час вони не могли повною мірою використовувати теоретичні положення цих досліджень з огляду на обмежені можливості ручного рахунку. Найчастіше при порівнянні комбінованої і роздільної схем енергопостачання міст і промислових центрів витрати в теплові мережі визначаються на основі узагальнених залежностей капіталовкладень в теплові мережі від укрупнених показників теплоплотності теплофіціруемих районів. При використанні таких методів не враховуються поступовість зростання теплових навантажень споживачів по роках розрахункового періоду, наявність існуючих ділянок мережі і не оптимізуються діаметри по ділянках теплових мереж з урахуванням технічних обмежень на тиску в вузлових точках мережі, різних питомих капіталовкладень по її ділянках, що може призводити до істотних прорахунків і помилок. Застосування ЕОМ відкриває великі можливості для створення нових, більш досконалих і точних методів оптимізації розвитку теплових мереж [26, 41, 42, 50, 65].
Завдання оптимізації теплових мереж може вирішуватися як без урахування, так і при обліку поступовості зростання теплових навантажень по роках розрахункового періоду. У разі, якщо фактор динаміки не враховується, постановка задачі може бути сформульована таким чином. Задано: розрахункові витрати води у споживачів; довжина ділянок і конфігурація теплової мережі; область допустимих значень питомої падіння напору в головній магістралі; термін служби існуючої теплової мережі і діаметри по її окремих дільницях; шкала стандартів можливих діаметрів теплової мережі; допустимий наявний напір на вводі у абонентів; технічні обмеження на тиск в вузлових точках мережі. Потрібно визначити: оптимальні значення діаметрів по ділянках мережі; кількість, місця розташування і параметри підкачуючих і дросселирующих підстанцій, відповідні мінімального значення цільової функції, в якості якої приймаються наведені витрати в теплову мережу входять до величину капіталовкладення /Ст.с обчислюються за формулою:


Оптимізація параметрів теплової мережі, т. Е. Знаходження мінімуму функції приведених витрат із застосуванням математичного моделювання і ЕОМ, може виконуватися такими методами:
1) перебір досить великого числа варіантів з різними значеннями питомої падіння тиску у напрямку головної магістралі за умови лінійного закону падіння тиску за цим напрямком (лінійний метод);
2) метод, заснований на застосуванні динамічного програмування (нелінійний метод).
У загальному вигляді математична постановка задачі оптимізації теплової мережі при використанні лінійного методу може бути записана так. знайти:

Лінійний метод оптимізації теплової мережі полягає в повному переборі заданих значень питомої падіння напору (h) в головній магістралі мережі, прийнятого однаковим на всіх її ділянках, і в знаходженні його оптимальної величини, що відповідає мінімуму критеріальною функції. При обчисленні / г (ШТ необхідність перебору всіх його значень (з заданим кроком), що лежать у межах, дозволених області, викликається тим, що залежність 3 = f (h) не характеризується суворої плавної монотонністю, т. Е. Можуть мати місце локальні мінімуми. Можливість їх появи викликається дискретністю діаметрів труб і типорозмірів будівельних конструкцій, а також наявністю ділянок в країнах, що розвиваються теплових мережах. при цьому локальні мінімуми будуть відповідати тим варіантам, при яких існуючі дільниці не перекладаються. при застосуванні пов ого методу в результаті розрахунку на ЕОМ можна отримати не один оптимальний варіант, а набір ряду варіантів, які не дуже відрізняються від оптимального за приведеними витратами. Це дозволяє проектувальнику вибрати варіант не тільки по формальному критерію мінімуму приведених витрат, але і з урахуванням експлуатаційних вимог, наприклад гідравлічної стійкості і надійності.
Допущення про лінійність закону падіння напору уздовж головної тепломагістралі спрощує розрахунок теплової мережі і в той же час вносить похибку у результати її оптимізації. Наприклад, лінійний метод не дозволяє в повній мірі врахувати відмінності в способах прокладки трубопроводів для різних ділянок мережі. У разі оптимізації розвивається мережі з існуючими ділянками такий метод не дозволяє врахувати важливу особливість, яка полягає в тому, що для нових ділянок мережі оптимальні значення питомої втрати тиску, як правило, менше, ніж для існуючих. Це пояснюється тим, що в мережах з існуючими ділянками більше частка витрат на перекачку теплоносія в сумарних витратах по тепловій мережі.
Нелінійний метод оптимізації теплових мереж заснований на поділі головної магістралі мережі на окремі ділянки з покрокової оптимізацією мережі по окремих дільницях [26]. При цьому методі замість знаходження мінімуму функції приведених витрат по всій мережі, що залежать від діаметрів усіх ділянок, що потребує вирішення складної системи рівнянь, послідовно знаходяться оптимальні рішення для окремих ділянок мережі.
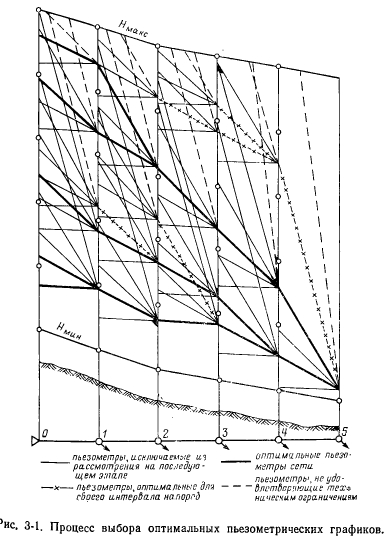
Основні вихідні положення методу динамічного програмування і послідовність виконання завдання при його застосуванні вище розглянуті на прикладі оптимізації складу і термінів введення обладнання ТЕЦ. В даному випадку покроковий процес будується з урахуванням особливостей задачі оптимізації теплової мережі. За основу (фазову змінну) приймається натиск, який розбивається на ряд значень (в заданих пределах- від мінімального до максимально допустимого значення), що утворюють вузли решітки. При переборі варіантів на кожному кроці і обчисленні наведених витрат для даного i-го напору Я, значення Я, приводиться у відповідність з найближчим стандартним діаметром. Покроковий процес оптимізації, принципову послідовність застосування якого пояснюють побудови рис. 3-1 [26], починається з останньої ділянки у, так як натиск в кінці мережі передбачається відомим. При цьому розглядаються всі можливі рішення для даної ділянки, що відповідають стандартним значенням діаметра. Рішення, при яких натиск в початковому вузлі даної ділянки виходить за межі допустимого діапазону, в подальшому не враховуються. Якщо в один вузол решітки потрапляє кілька значень діаметра, то за критерієм мінімуму приведених витрат визначається оптимальне рішення для цього вузла
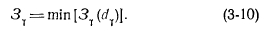
На наступному кроці враховуються в розрахунках дві ділянки - останній у і передостанній (у-1), при цьому розглядаються можливі рішення для ділянки (у-1), що є продовженням оптимальних рішень для кожного вузла решітки, отриманих на попередньому кроці. Якщо в один вузол решітки потрапляє кілька рішень (ймовірність цього значно більше, ніж на першому кроці), то визначається оптимальне рішення для двох ділянок у і (у-1):
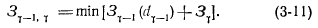
Шляхом додавання до вже розглянутих чергового (в порядку розташування) ділянки теплової мережі процес оптимізації повторюється. Таким чином, на кожному кроці в якості фазового змінної, по якій проводиться оптимізація, приймається діаметр початкового ділянки оптимізується частини мережі. При цьому число можливих рішень, фіксованих для даного кроку, при переході до наступного кроку (дільниці теплової мережі), як правило, менше числа вузлів решітки, х. е. числа заданих значень напору в мережі, яке залишається одним і тим же протягом усього покрокового процесу оптимізації. Остаточне рішення в цілому по мережі вибирається після завершення цього процесу і порівняння між собою за величиною сумарних приведених витрат всіх отриманих «траєкторій», т. Е. Можливих варіантів, число яких не перевищує заданого числа значень напору в мережі. Обгрунтованість застосування динамічного програмування для оптимізації теплових мереж показана в [26].
Нелінійний метод оптимізації дозволяє врахувати технічні і вартісні характеристики кожної ділянки мережі, вибирати оптимальні місця спорудження та параметри насосних підстанцій, оптимізувати розвиваються мережі з існуючими ділянками. Цей метод, заснований на покрокової оптимізації, застосуємо для розгалужених мереж як з одним, так і з декількома джерелами тепла, по але може бути використаний для оптимізації кільцевих мереж, так як в цих мережах в залежності від діаметра на одній з ділянок змінюються витрати води на інших ділянках мережі. Як нелінійний, так і лінійний методи оптимізації можуть бути застосовані для кільцевих мереж тільки в тих випадках, коли з допустимою похибкою кільцева мережа може бути перетворена в радіальну і попередньо задано в ній потокораспределение.
Для оцінки порівняльної ефективності різних методів оптимізації проводилися розрахунки теплових мереж різної конфігурації трьома методами: методом, широко поширеним в даний час в проектній практиці і заснованим на використанні нормативів і ручного рахунку (а); методом оптимізації, заснованим на передумові про доцільність зміни напору в головній магістралі за лінійним законом ( «лінійний метод») при виконанні розрахунків на ЕОМ (б); методом оптимізації на основі динамічного програмування ( «нелінійний метод») при виконанні розрахунків на ЕОМ (в).
Хрілев Л. С., Смирнов І. А. / Оптимізація систем теплофікації і централізованого теплопостачання / Под ред. Е. Я. Соколова.- М .: Енергія, 1978.




