Використання штучних нейронних мереж для розв'язання обернених задач електроімпедансной і магнітоіндукціонний томографії

1. ВИКОРИСТАННЯ штучних нейронних мереж ДЛЯ ВИРІШЕННЯ ЗВОРОТНИХ ЗАВДАНЬ електроімпедансних І магнітоіндукціонний...
2. 1. Введення
3. 2. М етод
4. 3. Результати
5. 4. Висновки
6. список літератури

ВИКОРИСТАННЯ штучних нейронних мереж ДЛЯ ВИРІШЕННЯ ЗВОРОТНИХ ЗАВДАНЬ електроімпедансних І магнітоіндукціонний ТОМОГРАФІЇ

Наша команда-партнер Artmisto

А. В. Корженевський

Інститут радіотехніки й електроніки РАН

Отримано 27 грудня 2001 р

Рішення проблеми реконструювання просторового розподілу абсолютної електропровідності ( "статичної" візуалізації) з високим просторовим дозволом за результатами вимірювань збурень квазістаціонарного електромагнітного поля, що проводяться поза досліджуваного об'єкта, відкриває широкі перспективи для застосування методів електроімпедансной томографії (ЕІТ) і магнітоіндукціонний томографії (МІТ) в медицині і інших областях. Жоден з існуючих методів розв'язання оберненої задачі тут не дає поки задовільних результатів в досягненні обох цілей (статичної візуалізації і задовільного просторового дозволу) одночасно в разі вимірювань, проведених in vivo. Ми досліджували можливість використання штучних нейронних мереж, яких навчають методом навчання з учителем, для поліпшення статичної візуалізації в низькочастотної електромагнітної томографії. Для прискорення навчання мереж і спрощення оцінки ступеня їх адекватності розв'язуваної проблеми, навчальні набори даних створювалися за допомогою комп'ютерного моделювання вимірювань. В процесі роботи тестувалися і порівнювалися різні алгоритми оптимізації і структури нейронних мереж. В результаті були отримані мережі, що демонструють високу якість реконструювання для модельних вхідних даних з довільним просторовим розподілом електропровідності як для ЕІТ, так і для МІТ. Статичні зображення задовільної якості були реконструйовані і з експериментальних даних, виміряних in vivo. Зокрема, в роботі демонструється зображення голови добровольця, отримане методом магнітоіндукціонний томографії. Показано, що задовільні статичні зображення можуть бути реконструйовані навіть з використанням одношарових лінійних штучних нейронних мереж.

1. Введення

Низькочастотна електромагнітна томографія це інтроскопічних метод, за допомогою якого може бути реконструйовано розподіл електричного імпедансу всередині об'єкта, такого як тіло людини, за результатами вимірювань квазістаціонарного ( "м'якого") електричного або магнітного поля, обуреного об'єктом. Завдання реконструювання зображень в низькочастотної електромагнітної томографії, такий як електроімпедансних томографія (ЕІТ) або магнітоіндукціонний томографія (МІТ), є прикладом нелінійної некоректної оберненої задачі [ 1 - 3 ]. Здійснення статичної ( "безопорной") візуалізації і досягнення високого просторового дозволу є ключовою проблемою для впровадження таких методів в клінічну практику. Жоден з існуючих алгоритмів не дає задовільних результатів у вирішенні обох проблем одночасно в разі використання даних, виміряних in vivo (на реальному людському тілі). Ми досліджували можливість використання штучних нейронних мереж, яких навчають методом навчання з учителем, для підвищення якості статичної візуалізації в такий томографії "м'яким полем". Перші успішні результати використання штучних нейронних мереж для реконструювання зображень в ЕІТ були опубліковані в [ 4 ], Де т.зв. Адаптивні Лінійні Елементи (лінійні нейронні мережі) були використані для динамічної візуалізації (візуалізації змін) електропровідності як для симульованих, так і для експериментальних вхідних даних. Ми спробували розширити застосування нейронних мереж і використовувати їх для статичної візуалізації в електроімпедансной і магнітоіндукціонний томографії.

Штучна нейронна мережа являє собою сукупність відносно простих однотипних обчислювальних вузлів (нейронів), пов'язаних один з одним численними налаштованим зв'язками [ 5 ]. Робота нейронної мережі зводиться до формування деякого корисного вихідного набору даних у відповідь на сукупність вхідних даних, тобто реалізації деякого функціонального перетворення даних. Властивості мережі визначаються не стільки властивостями нейронів, скільки структурою і властивостями зв'язків між ними.

Процес настройки зв'язків з метою надання мережі необхідних властивостей називається навчанням нейронної мережі. Найбільш поширений метод навчання - навчання з учителем передбачає наявність набору пар вхідних та відповідних їм бажаних вихідних даних, званого навчальної вибіркою. Використовуючи невязку реального і бажаного відповіді мережі для всіх прикладів навчальної вибірки, оптимізують зв'язку мережі, мінімізуючи цю невязку. Для того, щоб зробити рішення стійким до можливих шумів і помилок в даних вимірювань, до вхідних даних навчальної вибірки в процесі навчання додається шумова компонента.

У багатошарових нейронних мережах нейрони організовані в шари, так що пов'язаними між собою є тільки нейрони з суміжних шарів. Згідно з теоремою про апроксимації для двошарової мережі, перший шар якої складається з нейронів з нелінійної сигмоидальной передавальної функцією, а другий - з лінійних суматорів, для будь-якої неперервної функції довільного кінцевого числа аргументів існує кінцева нейронна мережа, апроксимуюча цю функцію з будь-який наперед заданою точністю. Таким чином, якщо зворотна задача, така як завдання електроімпедансной або магнітоіндукціонний томографії, має рішення (з необхідним ступенем регуляризації некоректної задачі), вона може бути вирішена за допомогою штучної нейронної мережі.

Нейронна мережа може складатися і з єдиного шару лінійних елементів. Така мережа може апроксимувати тільки лінійні залежності, проте часто простота створення і навчання таких мереж в сукупності з їх малою чутливістю до помилок масштабування вхідних даних робить виправданим їх застосування і для вирішення нелінійних задач, таких як зворотні завдання електромагнітної томографії. У наших експериментах ми використовували обидва типи мереж.

2. М етод

Для створення навчальних наборів даних для нейронних мереж, що виконують реконструювання зображень, використовувалося чисельне моделювання процесу вимірювання. Вихідні розподілу електропровідності в робочій області томографа генерувалися за допомогою генератора випадкових чисел з подальшою просторової фільтрацією фільтром низьких частот (використовувався Гауссовский фільтр) з метою зменшення вкладу високочастотних (дрібномасштабних) компонент. Навчальні набори даних складалися з 1 - 2 тисяч прикладів. Для додання нейронної мережі регулярізірующіх властивостей і здатності реконструювати зображення, використовуючи дані неідеальних вимірювальних систем, до вхідних даних в процесі навчання додавався шумовий сигнал, величина якого варіювалася в інтервалі 0,5 - 5% від максимальної величини вхідного сигналу в вибірці. Такий шум може моделювати як реальну шумову компоненту у вхідних даних, так і такі непередбачувані фактори як неточність розташування електродів на тілі пацієнта і геометрія самого тіла.

Експерименти проводилися з двома типами штучних нейронних мереж: нелінійної двошарової мережею з сигмоидальной передавальної функцією нейронів прихованого шару і лінійними суматорами в вихідному шарі, а також з набором незалежних лінійних мереж, кожна з яких мала один вихід, відповідний яскравості одного пікселя реконструюється зображення.

Кількість нейронів у прихованому шарі двошарової мережі визначає здатність мережі апроксимувати необхідне перетворення. Вибір цієї кількості визначається в значній мірі досвідом і інтуїцією. Недостатня кількість нейронів робить виконання необхідної апроксимації мережею неможливим, а надмірна кількість зменшує генерализирующий (узагальнюючу) здатність мережі. Після декількох проб конфігурація мережі з 60 нейронами в прихованому шарі була визнана придатною для вирішення обернених задач ЕІТ з шістнадцятьма електродами і МІТ з шістнадцятьма індукторами і детекторами. Робота такої мережі описується виразом:

,

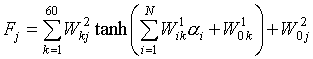де 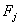- яскравість j -го пікселя реконструюється зображення, 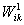і 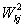- вагові матриці входів першого і другого шарів мережі, 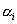- вхідні дані (результати вимірювань), N - кількість вхідних величин. Структура мережі показана на Мал . 1 . Навчання мережі проводилося методом зворотного поширення помилки. При цьому оптимізація методом сполучених градієнтів показала найкращі результати (швидкість і якість навчання).

Мал. 1. Структура двошарової штучної нейронної мережі використовується для ЕІТ і МІТ візуалізації: (1) - вхід (192 різниці потенціалів для 16-електродної ЕІТ системи з полярною инжекцией струму або 240 зрушень фаз для 16-катушечной МІТ системи); (2) - прихований шар (60 нейронів з сигмоидальной функцією збудження); (3) - вихідний шар (лінійні суматори), що представляє 164 пікселя зображення.

Структура лінійної мережі повністю визначається кількістю її входів і виходів. Лінійна мережа може бути створена і "навчена" за один крок з використанням методу найменших квадратів. Такі мережі дуже корисні для оцінки повноти навчальної вибірки. Крім того лінійність мережі робить її менш чутливою до неточностей масштабування даних, що вельми корисно, коли мережу, навчена за результатами двовимірного моделювання, використовується для реконструювання зображень за експериментальними даними. Для вирішення завдання візуалізації створювався набір лінійних мереж, що мають кількість входів рівне розміру вектора вхідних даних і один вихід, відповідний яскравості одного пікселя реконструюється зображення. Кількість таких мереж дорівнювала кількості пікселів в реконструйованому зображенні - 164 пікселя всередині реконструюється кругової області в наших експериментах. Їх функціонування описується виразом:

.

Проблема реконструювання ЕІТ зображень була розглянута для випадку шестнадцатіелектродной вимірювальної системи з полярною инжекцией струму. Пряма задача зводиться до вирішення рівняння Лапласа для неоднорідного середовища. Експериментальні дані були отримані за допомогою вимірювальної системи, описаної в [ 6 ]. Навчальний набір даних генерувався за допомогою двовимірної моделі кінцевих елементів для рівняння Лапласа в припущенні циліндричної геометрії досліджуваного об'єкта. Якість візуалізації за допомогою нейронних мереж порівнювався з результатами реконструювання методом зворотної проекції вздовж еквіпотенціалью електричного поля з синтезом опорного набору даних [ 6 , 7 ]. Архітектура нейронних мереж визначається кількістю вхідних сигналів (192 для 16-електродної ЕІТ з полярної инжекцией струму), кількістю вихідних пікселів (164) і кількістю нейронів в прихованому шарі (60).

У магнітоіндукціонний томографії вимірювання збурень змінного магнітного поля, викликаних вихровими струмами, використовується для визначення розподілу електропровідності всередині об'єкта [ 2 , 3 ]. В експериментальній вимірювальної системі [ 8 ] Використовується 16 індукторів і 16 детекторів магнітного поля, що оточують робочу область томографа. В якості вихідних даних для реконструкції зображень використовуються виміряні зрушення фаз між напругою, прикладеним до індуктора і напругою, вимірюваним кожним з детекторів. В даний час в якості основного алгоритму візуалізації використовується метод згортки і зворотного проекції вздовж ліній індукції невозмущенного магнітного поля. Цей лінійний метод дозволяє реалізувати тільки динамічну візуалізацію, т. Е. Візуалізацію змін розподілу електропровідності, що відбулися між двома послідовними вимірами. Використання штучної нейронної мережі могло б вирішити проблему статичної візуалізації в МІТ. Архітектура лінійної і нелінійної мереж, використаних для реконструювання зображень в МІТ, така ж як і мереж, використаних для випадку ЄІТ, за винятком кількості вхідних сигналів, що дорівнює 240 для 16-катушечной вимірювальної системи. При створенні навчальних наборів даних ми виходили з припущення про малому обуренні магнітного поля індуктора досліджуваної середовищем. Індуктор апроксимувати точковим магнітним диполем. Обурення магнітного поля індуктора провідним середовищем може бути наближено обчислено за допомогою наступного виразу:

,

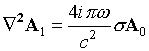де 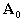і 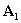- векторний потенціал невозмущенного магнітного поля і його обурення, викликаного провідним середовищем з провідністю 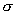. Взявши в якості 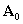векторний потенціал магнітного диполя, для амплітуди обурення індукції магнітного поля 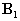отримаємо:

,

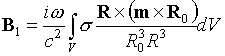де m - амплітуда магнітного моменту індуктора, 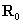- радіус-вектор з індуктора в точку інтегрування ( 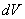), 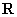- радіус-вектор з 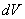в точку спостереження. Це рівняння справедливо при досить жорстких обмеженнях: мало впливав середовища на магнітне поле, нехтує внесок струмів зміщення в порівнянні з струмами провідності, мало впливав потенційного електричного поля на розподіл струмів (зокрема, відсутність ізоляційних бар'єрів всередині середовища). Проте такі обмеження є цілком виправданими в багатьох випадках при візуалізації біологічних об'єктів. Для створення навчальних наборів даних, як і в разі ЕІТ, використовувалися Фільтровані випадкові розподілу електропровідності. Відповідні вимірювані зрушення фаз обчислювалися потім для цих розподілів за допомогою описаного вище підходу.

3. Результати

3.1. електроімпедансних томографія

Результати статичної візуалізації тестових розподілів електропровідності, здійснюваної навченої двошарової нейронної мережею за даними, обчисленими за допомогою двовимірної моделі кінцевих елементів, досить обнадійливо - см. Мал. 2 . Збільшення рівня шуму у вхідних даних до розумних меж призводить лише до зменшення роздільної здатності, переважно в центрі зображення. Спроби реконструювати зображення з експериментально виміряних даних не привели, однак, до задовільних результатів, хоча метод зворотного проектування з синтезом опорних даних, який використовується в даний час в томографической системі, дає цілком задовільні зображення для тих же даних - Мал. 3 . Ймовірною причиною такої відмінності є відмінність просторових залежностей полів в разі двох і трьох вимірів. Ця різниця робить некоректним використання мережі, навченої з використанням двовимірного моделювання, для роботи з експериментальними даними, відповідають реальному тривимірному світу. Зокрема, якщо відношення максимальної виміряної різниці потенціалів до мінімальної в тривимірному випадку становить приблизно 1 до 0.2 - см. Експериментальну криву на Мал. 4а , То в двовимірному випадку це відношення становить приблизно 1 до 0.6 - см. Результат моделювання на Мал. 4б .

Початкове розподіл електропровідності

ЕІТ НС візуалізація з 1% вхідним шумом

ЕІТ НС візуалізація з 2% вхідним шумом

приклад 1

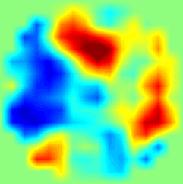
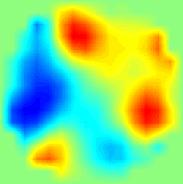
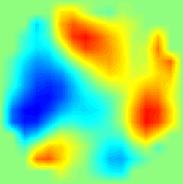
приклад 2

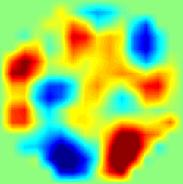
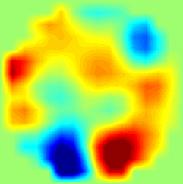
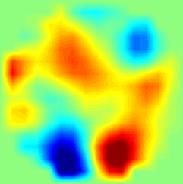
Рис 2. Результати статичної ЕІТ візуалізації випадкових розподілів електропровідності за допомогою двошарової нейронної мережі. В якості вхідних даних використані результати двовимірного моделювання з додаванням шумовий компоненти.

Мал . 3. Статична ЕІТ зображення грудної клітини добровольця реконструйоване методом зворотної проекції з синтезом опорних даних. Світлі тони відповідають високій електропровідності.

(А)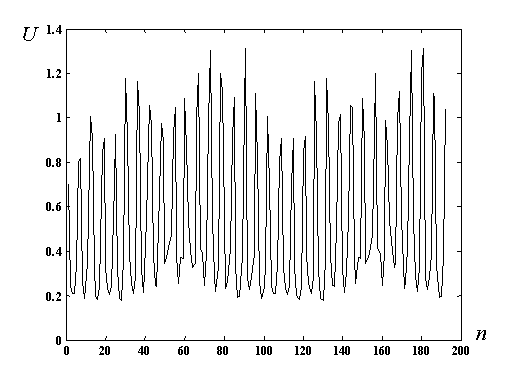

(Б)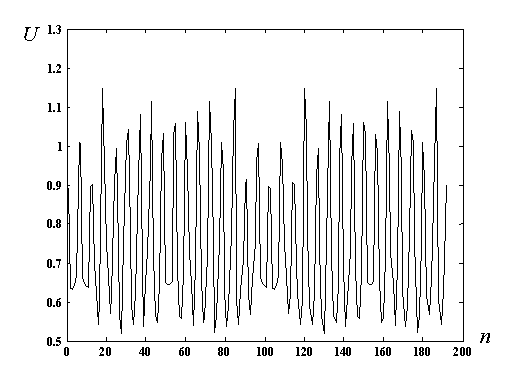

Мал . 4. Вхідні дані для ЕІТ реконструкції отримані шляхом вимірів на грудній клітці добровольця (а) і обчислені за допомогою двовимірної моделі, заснованої на методі кінцевих елементів, з використанням аналогічного просторового розподілу електропровідності (б). U - нормовані різниці потенціалів між сусідніми електродами, n - номер вимірювання згідно використовуваної стратегії вимірювань.

Набір лінійних нейронних мереж, навчених за результатами такого ж двовимірного моделювання, дає цілком задовільні результати візуалізації за тими ж експериментальними даними. Результат такої візуалізації показаний на Мал . 5 . Зображення виглядає деформованим - стягнутим до центру і неадекватним на периферії, проте все анатомічні структури, видимі на Мал. 3 , Є і на зображенні, реконструйованому нейронною мережею. Звичайно, лінійність нейронної мережі обмежує її здатність вирішувати нелінійну зворотну задачу, якою є завдання ЕІТ. Однак мала чутливість такої мережі до масштабу варіації вхідних даних виявилася життєво важливою в разі реконструювання зображень по тривимірним вхідних даних мережею, навченої за допомогою двовимірної моделі вимірювальної системи.

Мал. 5. статичність ЕІТ зображення грудної Клітини добровольців реконструйоване лінійної нейронних мереж, навченої с помощью двовімірної конечноелементной моделі. Використані ті ж вхідні дані, що і для рис. 3.

3.2. магнітоіндукціонний томографія

Результати візуалізації за допомогою двошарової нелінійної мережі для модельних вхідних даних показані на Мал. 6 , Де кілька випадкових розподілів електропровідності представлені в лівій колонці, а відповідні реконструйовані зображення при різному рівні шуму, доданого до вхідних даних, показані праворуч. Мережа демонструє можливість чудовою статичної візуалізації. Збільшення зашумленности вхідних даних призводить до зменшення роздільної здатності переважно в центрі зображення.

Початкове розподіл електропровідності

МІТ НС візуалізація з 1% вхідним шумом

МІТ НС візуалізація з 2% вхідним шумом

приклад 1

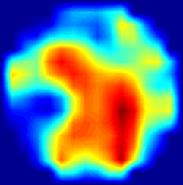
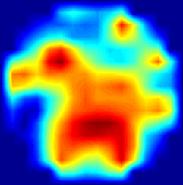
приклад 2

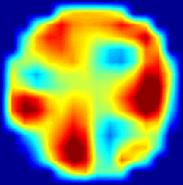
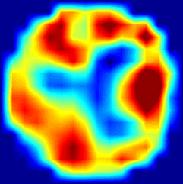
Мал . 6. Результати статичної МІТ реконструкції випадкових розподілів електропровідності при різних рівнях вхідного шуму за допомогою двошарової нейронної мережі.

Статична візуалізація розподілу електропровідності всередині протяжних об'єктів зажадала більшої точності вимірювань, ніж використовувалася раніше динамічна візуалізація методом згортки і зворотного проекції. Перші експерименти по in vivo МІТ статичної візуалізації виявилися не дуже успішними через недосконалість вимірювальної системи. Після додаткового екранування індукторів, помітно зменшив впливу ємнісного зв'язку між індукторами і детекторами, були отримані перші стабільні і відтворювані статичні МІТ зображення за результатами вимірювань, проведених in vivo. Зображення були реконструйовані за допомогою штучної нейронної мережі. Зокрема, таке зображення голови добровольця наведено на Мал. 7 . Два яскравих плями в центральній ділянці об'єкту відповідають регіонах з високою електропровідністю і можуть бути ідентифіковані як шлуночки мозку, заповнені спинномозковою рідиною. Електропровідність спинномозкової рідини в 5 - 10 разів перевершує електропровідність інших тканин мозку [ 9 ] На робочій частоті вимірювальної системи (20 МГц). Це обумовлює високий контраст зображення.

Мал . 7. Статична МІТ зображення голови добровольця, реконструйоване за допомогою лінійної нейронної мережі. Потилицю знаходиться у верхній частині зображення, права сторона - в лівій частині зображення. Два червоних плями, відповідних областям високої електропровідності, можуть бути ідентифіковані як шлуночки мозку.

4. Висновки

Штучні нейронні мережі можуть бути використані для вирішення обернених задач електроімпедансной і магнітоіндукціонний томографії. Зокрема, тести з модельними і експериментальними даними демонструють принципову можливість статичної візуалізації задовільної якості з невисокими обчислювальними витратами. Статична візуалізація i n vivo реалізована за допомогою штучних нейронних мереж як в ЄІТ, так і в МІТ. Переваги описаних методів включають можливість досить тонкої регуляризації розв'язання оберненої задачі, яка може брати до уваги такі фактори, як невизначеність геометрії обстежуваного тіла. Для цього в навчальний набір даних повинні бути включені приклади з перекрученою випадковим чином формою кордону тіла.

Основною проблемою на шляху практичного застосування штучних нейронних мереж для візуалізації в низькочастотної електромагнітної томографії є ​​необхідність синтезу великих високоякісних навчальних наборів даних. Для вирішення цієї проблеми необхідно розробити реалістичних тривимірних моделей, заснованих на методі кінцевих елементів, для вирішення відповідних прямих задач.

Спрощені і двовимірні моделі для розв'язання прямої задачі можуть бути використані в поєднанні з лінійними нейронними мережами, менш чутливими до некоректних залежностей у вхідних даних, ніж багатошарові нелінійні мережі. Представлені результати демонструють хороші характеристики таких лінійних мереж навіть при вирішенні таких реально нелінійних задач, як завдання томографії "м'яким полем".

Робота виконана за підтримки Російського фонду фундаментальних досліджень, проект № 01-01-00982.

список літератури

[1] Barber D. C. and Brown B. H. Applied potential tomography // J. Phys. E: Sci. Instrum., 1984, v 17, p. 723-733

[2] Корженевский А.В., Черепеніна В.А. Магніто-індукційна томографія // РЕ, 1997, т. 42, N 4, с. 506-512

[3] Корженевский А.В., Черепеніна В.А. Магнітоіндукціонний томографія // Журнал радіоелектроніки, 1998, № 1, http://jre.cplire.ru/win/dec98/1/text.html

[4] Adler A. and Guardo R. A neural network image reconstruction technique for electrical impedance tomography // IEEE Trans. Med. Imag., 1994, v. 13, p. 594-600

[5] Caudill M. Neural Networks Primer, San Francisco CA: Miller Freeman Publications, 1989

[6] Корженевский А.В., Корнієнко В.М., Культіасов М.Ю., Культіасов Ю.С., Черепеніна В.А. Електроімпедансних томограф для медичних програм // ПТЕ, 1997, N 3, с. 133-140

[7] Korjenevsky AV Reconstruction of absolute conductivity distribution in electrical impedance tomography // Proc. 9th Int. Conf. On Electrical Bio-Impedance (Heidelberg, 1995), p. 532-535

[8] Korjenevsky A. , Cherepenin V. and Sapetsky S. Magnetic induction tomography: experimental realization // Physiol. Meas. , 2000., v. 21, p. 89-94

[9] Gabriel C. and Gabriel S. Compilation of the dielectric properties of body tissues at RF and microwave frequencies, Physics Department King's College London Report AL / OE-TR-1996-0037, http://niremf.iroe.fi.cnr.it/docs/DIELECTRIC/Report.html

Автор:
Корженевский Олександр Володимирович, к.ф.-м.н., с.н.с., Інститут радіотехніки й електроніки РАН, e- mail: korjenevsky @cplire .ru